Уравнения равновесия жидкости

Выделим в покоящейся жидкости вокруг точки А элементарный объ­ем в виде параллелепипеда и составим условия его равновесия.

На этот параллелепипед выделенной жидкости действуют поверхно­стные силы (силы гидростатического давления) и объемные силы.

Примем, что давление в центре параллелепипеда (в точке А) равно р_А. Тогда давление в центре левой грани р\ будет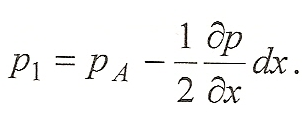

Сила давления на всю левую грань

Аналогично, сила давления на правую грань

Здесь —изменение гидростатического давления по оси х на единицу длины. Знак этой величины определяется направлением перемещения от точки А к соответствующим граням.

Проекция объемных сил на ось х будет равна 𝜌Хdxdy dz.

Тогда уравнение равновесия (покоя) выделенного объема жидкости можно записать в виде

Подставляя значения Р\ и и приводя подобные члены, имеем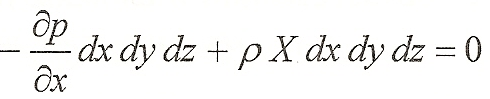

Сокращая на объем параллелепипеда dxdydz, получим уравнение для единицы объема жидкости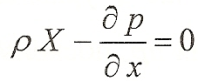

Уравнения для других осей запишем по аналогии:

Эти уравнения называются уравнениями Эйлера. В них заключаются необходимые и достаточные условия равновесия жидкости, так как если эти условия выполняются в любой точке жидкости, то каждая частица жидкости находится в равновесии.

Обычно систему дифференциальных уравнений равновесия (уравне­ния Эйлера) записывают в следующем виде:

Уравнения Эйлера показывают, что в состоянии покоя массовые си­лы, действующие на каждую частичку жидкости, уравновешиваются по­верхностными силами (градиентом давления).