Вывод формулы для координат центра давления на плоскую стенку.

Найдем координату центра давления на площадке со. Будем считать для простоты, что на стенку действуют только силы избыточного давле­ния, т. е.pо=0

Обозначим центр давления буквой D. Тогда его координата по стенке будет l_D. Вспомним теорему механики о том, что момент равнодействую­щей силы (в нашем случае - гидростатического давления) относительно оси (возьмем ось Ох) равен сумме моментов составляющих сил, т. е.

Из формулы dP = pо dω+ 𝜌gl sin a dω.определим величину dP и, с учетом того, что Ро = 0, получим

где J_x - момент инерции площадки со относительно оси х.

Отсюда: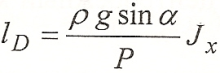

Подставим в эту формулу значение Р из выражения 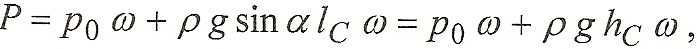и, учиты­вая, что ро = 0, получим:

Выразим момент инерции относительно оси х — J_x — через момент инерции относительно оси, проходящей через центр тяжести площадки со и параллельной осих —Jс: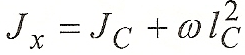

Тогда окончательно имеем (2.14)

Из этой формулы видно, что l_D всегда будет больше 1с, т. е. центр давления лежит глубже, чем центр тяжести площадки ω Величина имеет размер длины и называется эксцентриситетом давления.

Эксцентриситет давления уменьшается с увеличением глубины погруже­ния площадки.

Если площадь ω имеет ось симметрии, перпендикулярную оси х, то формула (2.14) полностью определяет положение центра давления. В слу­чае несимметричной фигуры нужно отыскать вторую координату центра давления в направлении, параллельном оси х. Построим ось у, перпенди­кулярную оси х, и проведем все расчеты и рассуждения, аналогичные вы­шеприведенным, относительно этой оси. Получим:

Здесь - центробежный момент инерции площадки ω относительно осей х и у. Следует иметь в виду, что центробежный момент

инерции может быть и положительным, и отрицательным, в зависимости от расположения оси у.

В предыдущих рассуждениях принято, что давление на поверхности жидкости /7о равно нулю. Если оно отлично от нуля, то учесть его можно так: точкой приложения силы внешнего давления на площадку будет центр тяжести этой площадки; точкой приложения избыточного давления явля­ется центр давления. Зная две этих силы и точки их приложения, можно найти общий центр давления на площадку, при этом полная сила давления на площадь ω будет равна сумме внешнего и избыточного давлений.

9. Давление на цилиндрические и сферические поверхности.

Рассмотрим открытый сосуд, заполненный покоящейся жидкостью. Одна из стенок сосуда имеет цилиндрическое очертание.

(.) 0 – центр кривизны поверхности.

В соответствии с I свойством гидростатического давления в каждой точке такой поверхности давление направлено по нормали. Следовательно, в случае цилиндрической (и сферической) поверхности направление результирующей силы давления P всегда проходит через центр кривизны поверхности.

В общем случае криволинейной поверхности с несколькими центрами кривизны это не выполняется – через центр кривизны поверхности в данной точке проходит только направление элементарных составляющих сил.

Результирующую силу давления P можно разложить на де составляющие:

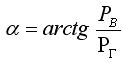Таким образом, дя определения величины и направления силы P необходимо определить Рв и Pг. Найдём Рв и Pг.

(7.2)

[1] Для этого выделим на рассматриваемой криволинейной поверхности элементарную площадку dw (Рис. 7.2). В связи с малостью её размеров её можно считать плоской. Центр площадки находится на глубине h.

[2] На эту площадку действует сила dP, обусловленная гидростатическим давлением в точке, соответствующей центру площадки. Как и ренее, пренебрегаем изменением давления при перемещении вдоль площадки в связи с малостью её размеров.

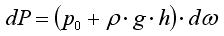
Горизонтальная составляющая силы dP: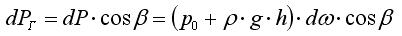

Из рисунка 7.2 видно, что - вертикальная проекция площадки dw

Таким образом:

Проинтегрируем последнее выражение по площади w поверхности сосуда, для того чтобы получить величину горизонтальной составляющей силы давления на эту поверхность. поскольку - статический момент вертикальной проекции площади dw относительно оси OX. (В данном случае ось OX направлена нормально к плоскости чертежа, она находится на прямой, образованной пересечением цилиндрической поверхности и плоскостью свободной поверхности жидкости).

hc – глубина погружения центра тяжести вертикальной проекции площади w.

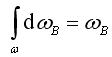- вертикальная проекция площади w (сумма вертикальных проекций элементарных площадок dwв).

Таким образом: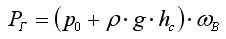

Это утверждение можно распространить и на случай других криволинейных поверхностей (нецилиндрических).

Вертикальная составляющая силы давления dP на элементарную площадку: (*)

аналогично - горизонтальная проекция площадки dw.

Для определения величины вертикальной составляющей силы давления на рассматриваемую поверхность проинтегрируем (*) по площади w.

где

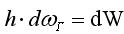– объём жидкости, находящийся над элементарной площадкой dw;

– объём жидкости, находящийся над криволинейной поверхностью – объём тела давлении

– горизонтальная проекция площади криволинейной поверхности;

- вес тела давления.

Итак:

Это утверждение также можно распространить и на случай других криволинейных поверхностей (нецилиндрических).

Зависимости, полученные для величин горизонтальной и вертикальной составляющих силы гидростатического давления на криволинейные поверхности справедливы также и для плоских поверхностей.

случае определения составляющих силы избыточного гидростатического давления при давлении на поверхности жидкости равном атмосферному, давление на поверхности жидкости следует принимать равным нулю.

Основные понятия гидродинамики

В разделе «гидродинамика» изучаются законы движения жидкости.

Движение несжимаемой жидкости характеризуется величинами давления и скорости (в случае несжимаемой жидкости плотность можно считать постоянной).

Виды движения жидкости.

В движущейся жидкости скорость v и давление p могут изменяться в пространстве и во времени: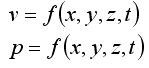

в связи с этим различают виды движения:

Неустановившееся – вид движения, при котором давление и скорость изменяются во времени и в пространствеУровень в сосуде будет падать и скорость потока будет изменяться во времени. Одновременно с каждый момент времени скорость v в разных частях трубопровода из за его сужения будет разной (так же как и давление p).

Установившееся (стационарное) – вид движения, при котором давление и скорость постоянны во времени, а изменяются только в пространстве.

В сосуд добавляют воду по мере её вытекания, таким образом скорость изменяется только из-за сужения трубопровода (увеличивается к концу), то есть изменяется только в пространстве.

Скорость и давление в каждой точке потока постоянны.

Равномерное – вид движения, при котором давление и скорость постоянны во времени и в пространстве.

Также различают напорное и безнапорное движение жидкости.

Напорное движение – в потоке отсутствует свободная поверхность.

Безапорное движение – в потоке имеется свободная поверхность.

Линия тока – воображаемая линия, проведённая в потоке, таким образом, что в каждой её точке направление скорости совпадает с касательной к этой линии.То есть, если известны линии тока, то если в любой их точке провести касательную, её направление совпадёт с направлением скорости.

При неустановившемся движении линии тока изменяются во времени.

При установившемся движении линии тока постоянны во времени.

Элементарная струйка тока.

Рассмотрим безграничный поток жидкости.

Œ Выделим в этом потоке элементарную площадку dw. Площадка dw настолько мала, что в её пределах скорость потока жидкости проходящего сквозь неё можно считать одинаковой для всех её точек. Через каждую точку контура, ограничивающего площадку dw проведём линию тока. Эти линии тока в совокупности составляют поверхность тока.В связи с тем, что скорости в каждой точке такой поверхности направлены по касательной (так как поверхность образована линиями тока), сквозь поверхность тока перемещения жидкости не происходит.((часть потока, ограниченная поверхностью тока и есть элементарная струйка))

Элементарной струйкой называется часть потока, ограниченная линиями тока, проведёнными через все точки жидкого контура, заключающего в себе элементарную площадку.

Таким образом, поток жидкости можно рассматривать как совокупность элементарных струек.При установившемся движении элементарная струйка обладает следующими свойствами:

1. Положение элементарной струйки неизменно в пространстве.

2. Отсутствует переток жидкости через боковую поверхность элементарной струйки.

3. Скорости во всех точках одного поперечного сечения элементарной струйки одинаковы.

Геометрические характеристики потока жидкости.

Живое сечение потока – поверхность, проведённая таким образом, что она оказывается нормальна к линиям тока.

Цилиндрический поток Нецилиндрический поток

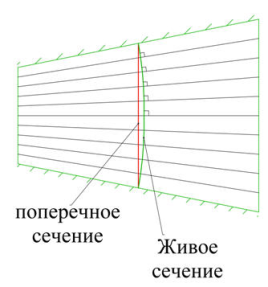
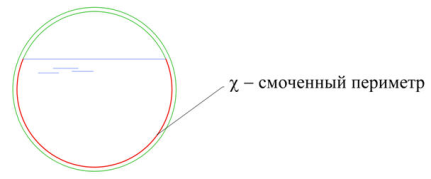Смоченный периметр – часть периметра, находящаяся в контакте с жидкостью.

При напорном движении смоченный периметр и геометрический периметр совпадают. Смоченный периметр – та область сечения потока в которой действуют силы внешнего трения.

Гидравлический радиус потока – отношение величины площади живого сечения потока w к его смоченному периметру c. (8.1)

Для напорного движения в трубопроводе круглого сечения радиусом r:

Таким, образом гидравлический радиус характеризует форму потока жидкости.

Расход жидкости – объём жидкости W, проходящий через живое сечение потока в единицу времени t.