Граничная концентрация неосновных носителей в базе

Анализ работы активных элементов ИС (диод, биполярный транзистор) показывает, что их характеристики во многом определяются концентрацией и распределением неосновных носителей в базе. Другими словами, необходимо знать выражение для граничной концентрации неосновных носителей в базе и закон ее распределения.

Запишем уравнение полной плотности тока для дырок

.

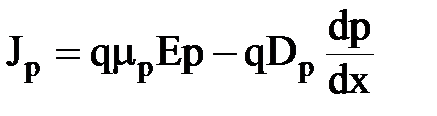(1.22)

Учитывая, что E = – dj/dx, где j — электростатический потенциал вдоль образца, и что D = mkT/q, запишем(1.23)

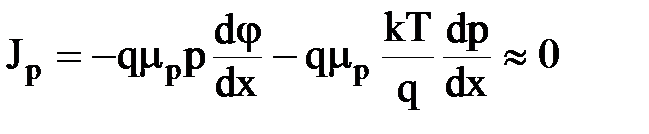
(1.23)

Будем считать, что ток, плотность которого для дырок равна J_p, мал настолько, что справедливо неравенство: J_p << qD_p×dp/dx.

Если отсчитывать потенциал относительно р-области (р-область "заземлена"), тo наличие внешнего смещения в прямом направлении приводит к повышению средней энергии электронов в n-области на величину qU. Поэтому, как показано на рис.1.3, б, высота потенциального барьера уменьшится и станет равна q(j_k–U) .

Следовательно, выражение (1.23) можно записать

(1.24)

где p_n(0) — концентрация дырок в n-области на границе перехода x = x_n, т.е. p_n (0) = p_nгр.

Решая это уравнение и зная, что (см.(1.7),получим

Аналогично .

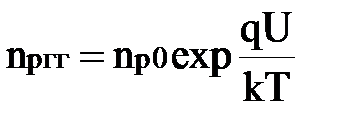(1.25)

При решении выражений(1.22) считали, что концентрации основных носителей вне области объемного заряда, при условии малости токов, практически равны равновесной. Величина напряжения U на р-n-переходе подставляется в(1.25) со знаком "+" при прямом смещении p-n-перехода и "–" при обратном.