Вопрос №37

Напряженность электростатического поля - векторная величина.

Напряженность электрического поля:

E = F/Q пробный

Напряженность электростатического поля (точечного заряда):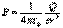

где r - расстояние от заряда Q, создающего поле, до точки поля, в которой определяется напряженность.

Единица напряженности - вольт на метр (В/м)

Гаусса — Остроградского

Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:

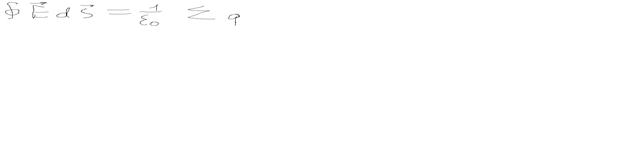
то есть интеграл от дивергенции векторного поля 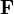, распространённый по некоторому объёму , равен потоку вектора через поверхность 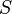, ограничивающую данный объём.