Основные формулы. Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме

Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q₁ и Q₂ и обратно пропорциональна квадрату расстояния r между ними:

где k — коэффициент пропорциональности, зависящий от выбора системы единиц.

Сила 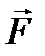направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F < 0) в случае разноименных зарядов и отталкиванию (F > 0) в случае одноименных зарядов. Эта сила называется кулоновской силой.

В СИ коэффициент пропорциональности равен

k = 1/ 4πε₀

Тогда закон Кулона запишется в окончательном виде:

Величина называется электрической постоянной; она относится к числу фундаментальных физических постоянных и равна = 8,85×10^-12Кл²/(Н×м²), или

ε₀ = 8,85*10^-12 Ф/м

где фарад (Ф) — единица электрической емкости.

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный заряд, помещенный в эту точку поля:

Таким образом, напряженность поля точечного заряда в вакууме

или в скалярной форме:

Величина

называется потоком вектора напряженности через площадку dS. Здесь — вектор, модуль которого равен dS, а направление совпадает с направлением нормали 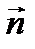к площадке.

Принцип суперпозиции (наложения) электростатических полей: напряженность результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности:

Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на .

§ поле равномерно заряженной бесконечной плоскости:

§ поле двух бесконечных параллельных разноименно заряженных плоскостей: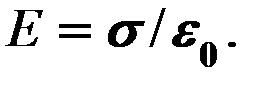

§ поле равномерно заряженной сферической поверхности:

§ поле объемно заряженного шара:

§ поле равномерно заряженного бесконечного цилиндра (нити): .

Работа при перемещении заряда g_o из точки 1 в точку 2

Потенциальная энергия заряда g_o, находящегося в поле заряда g на расстоянии r от него, равна

Потенциал в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.

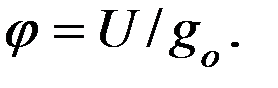
Работа, совершаемая силами электростатического поля при перемещении заряда g_o из точки 1 в точку 2, может быть представлена как

Если перемещать заряд g_o из произвольной точки за пределы поля, т. е. в бесконечность, где по условию потенциал равен нулю, то работа сил электростатического поля, согласно , откуда

Для уединенного проводника можно записать

Величину называют электроемкостью (или просто емкостью) уединенного проводника.

Емкость шара:

Емкость плоского конденсатора:

1. Параллельное соединение конденсаторов. У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна . Если емкости отдельных конденсаторов С₁, С₂, ..., С_n, то их заряды равны:

…………………………….

а заряд батареи конденсаторов

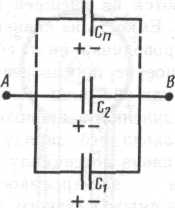
Рисунок 6

Полная емкость батареи:

т. е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.

2. Последовательное соединение конденсаторов. У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи

где для любого из рассматриваемых конденсаторов

Рисунок 7

С другой стороны,

откуда

т. е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.