
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 4. Человек стоит в центре скамьи Жуковского (рисунок 3) и вращается с частотой ν1=0,5 об/с
Человек стоит в центре скамьи Жуковского (рисунок 3) и вращается с частотой ν1=0,5 об/с. Момент инерции человека и скамейки относительно оси вращения I=6 кг*м2. В вытянутых в стороны руках человек держит гири массой m=2 кг каждая. Расстояние между гирями L1= 1,6 м. Сколько оборотов в секунду будет делать скамейка с человеком, если он опустит руки и расстояние между гирями станет равным L2=0.4 м?
| L1 |
| L2 |
Рисунок 3
| Дано: ν1=0,5 об/с I=6 I=6 кг*м2 m=2 кг L1= 1,6 м L2=0.4 м |
| ν2 - ? |
Решение:
В данной системе трением пренебрегаем, а моменты внешних сил тяжести и реакции опоры будем считать уравновешенными, для системы человек - скамья - гири будет выполняться закон сохранения момента импульса:
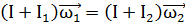
или в скалярной форме (  совпадают по направлению):
совпадают по направлению):

где I- момент инерции человека и скамейки;
I1- момент инерции гирь в 1-м положении;
ω1- угловая скорость системы в 1-м положении;
I2- момент инерции во 2-м положении;
ω 2- угловая скорость системы во 2-м положении.
Выразим угловую скорость со через частоту  :
:
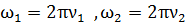
Момент инерции гири определяется по формуле момента инерции материальной точки: I = mr2. Гирь в нашем случае две, r = L/2, поэтому:


Подставляя выражения для ω1, ω2, I1 и I2 в равенство (1), получим:
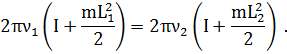
Отсюда определим:
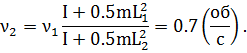
Проверка размерности:

Ответ: ν1=0,7 об/с.
Дата добавления: 2015-02-09; просмотров: 714; Мы поможем в написании вашей работы!; Нарушение авторских прав |