
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 1.
Через блок, укрепленный на горизонтальной оси, проходящей через его центр, перекинута нить, к концам которой прикреплены грузы 
и 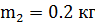 . Масса блока
. Масса блока  . Блок считать однородным диском. Найти ускорение грузов.
. Блок считать однородным диском. Найти ускорение грузов.
Да Дано:

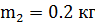

|

|
ГГ Решение:
С Система состоит из трех тел: грузов  и
и  , движущихся постуательно, и блока m, вращающегося относительно неподвижной оси, проходящей через центр масс блока. Груз
, движущихся постуательно, и блока m, вращающегося относительно неподвижной оси, проходящей через центр масс блока. Груз  находится под действием двух сил: силы тяжести m1
находится под действием двух сил: силы тяжести m1  и силы натяжения нити
и силы натяжения нити  . Груз
. Груз  также находится под действием двух сил: силы тяжести
также находится под действием двух сил: силы тяжести  и силы натяжения нити
и силы натяжения нити  . Запишем 2-й закон Ньютона для грузов:
. Запишем 2-й закон Ньютона для грузов:
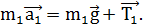

Блок вращается вокруг неподвижной горизонтальной оси, проходящей через его центр, следовательно, момент силы тяжести блока и момент силы реакции оси равны нулю. Если предположить, что нить не скользит относительно блока, то вращают блок только силы натяжения нити.
Запишем основное уравнение динамики вращательного движения для блока:
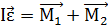
где 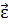 – угловое ускорение,
– угловое ускорение,
 – момент инерции блока,
– момент инерции блока,
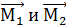 – моменты сил
– моменты сил  .
.
Если нить невесома, то силы натяжения вдоль нити с каждой стороны блока одинаковы по модулю, то есть:

Ускорения обоих грузов считаемравными по модулю. Если нить не проскальзывает относительно блока, то касательное ускорение его точек, соприкасающихся с нитью, равно ускорению нити в любой ее точке и ускорению грузов:

Для перехода к скалярным соотношениям для описания движения грузов введем ось Y. Теперь векторные уравнения можно заменить скалярными:

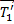
|
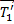
|

|
|

|

|
| Y |
Рисунок 1
Моменты сил  и
и  направлены по оси вращения, но в противоположные стороны. Примем направление вектора
направлены по оси вращения, но в противоположные стороны. Примем направление вектора  за положительное. Тогда момент силы
за положительное. Тогда момент силы  относительно оси вращения будет положительным, а момент силы
относительно оси вращения будет положительным, а момент силы  - отрицательным. Векторное уравнение можно переписать в виде:
- отрицательным. Векторное уравнение можно переписать в виде:

или
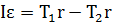
где r- радиус блока.
Учитывая, что момент инерции однородного диска: 
и связь линейного и углового ускорений:  ,
,
получаем:


Из уравнений выразим силы натяжения нитей:
 ,
,

Подставив значения, получим:
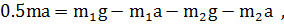


Проверим размерность:

Вычисления:
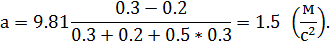
Ответ: а=1,5 
Дата добавления: 2015-02-09; просмотров: 390; Мы поможем в написании вашей работы!; Нарушение авторских прав |