Загальний випадок дії сил на брус

Як приклад більш загального випадку складного опору розглянемо розрахунок колінчастого вала. Для нього в ряді перетинів має місце одночасна дія осьових сил, крутні і згинальні моменти.

Досліджуємо випадок роботи найбільш простого вала. Вал (рис. 14, а) складається із шатунної шийки 3, двох щік 2 і двох корінних шийок 1, щоопираються на корінні підшипники. Всі необхідні розміри вала зазначені на кресленні.

На шатунну шийку 3 з боку шатуна діє під кутом до горизонтальної осі у сила Р₂=10 кН. Момент цієї сили щодо осі обертання врівноважується крутним моментом М на маховику. Вага маховика G = 5 кН.

а	б

Рис. 14. Розрахунок колінчатого вала

При заданих умовах необхідно визначити розміри перетинів вала й шатунної шийки, а також призначити розміри прямокутного перетину щік залежно від більшого з діаметрів по співвідношеннях ; , після чого провести перевірочний розрахунок на міцність. Прийняти допустиме напруження . Розрахунок вести по IV теорії міцності.

Від заданої конструкції переходимо до розрахункової схеми. Насамперед необхідно визначити реакцію в підшипниках, а також, крутний момент, на маховику. Для цього розкладемо силу на горизонтальну і вертикальну складову :

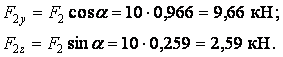
Реакції в опорах також можна представити у вигляді двох проекцій — , і , . Їх величини знаходимо з рівнянь рівноваги

Переходимо до побудови епюр згинальних моментів. Обчислю ординати епюри моментів (у площині xOz):

для I ділянки

для II ділянки

для III ділянки

для IV ділянки

для V ділянки

для VI ділянки

для VII ділянки

Відкладаючи обчислені ординати, будуємо епюру (рис. 14, б).

Аналогічно обчислюємо ординати і будуємо епюри згинальних моментів і , що діють у площинах хОу й yOz, а також епюру крутних моментів .

У результаті зіставлення епюр встановлюємо, що небезпечними є наступні перетини:

для вала – перетин у нижнього кінця лівої щоки (рис. 15), причому

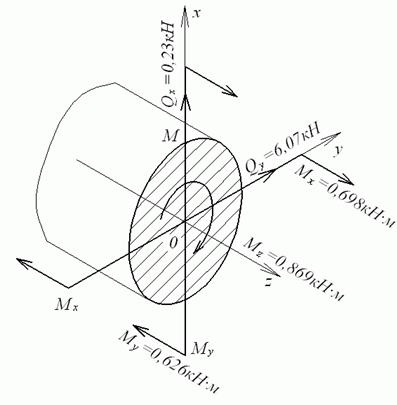
Рис. 15. Небезпечний переріз вала

для щік – нижній перетин лівої щоки (рис. 16), причому

Рис. 16. Небезпечний переріз щоки

для шатунної шийки – середній її перетин, причому

Визначення діаметрів вала й шатунної шийки. Розрахунок на міцність круглого бруса при вигині із крутінням по IV теорії виконується по формулі :

(24)

При вал повинен мати момент опору

Прийнявши приблизно , знайдемо діаметр вала:

Шатунна шийка повинна мати момент опору

тоді її діаметр

Призначаємо для шатунної шийки і вала однаковий діаметр перетину:

Перевірочний розрахунок щоки. Відповідно до умови задачі підбираємо розміри перетину щоки такими: ; . Переходячи до перевірки міцності прийнятого перетину щоки, обчислимо його геометричні характеристики:

Перевіряти на міцність у небезпечному перерізі прямокутну щоку, що працює на вигин із крутінням (рис. 10.39), треба в декількох точках – K, S і L.

У точці K по формулі (22):

У точці S по формулі (20):

У точці L по формулі (10.84):

Таким чином, самою небезпечною є точка L, але і у ній набільше нормальне напруження допускається менше

Оцінка впливу поперечних і поздовжніх сил. Облік поздовжніх і поперечних сил при підборі перетину надзвичайно ускладнив би розрахунок. Тому що додаткові напруги від дії поперечних сил звичайно невеликі, то при підборі перетину ними зневажаємо. Найбільш просто оцінити їх вплив, перевіряючи перетин після його підбора.

У небезпечному перерізі вала (рис. 10.38) крім врахованих при підборі перетину моментів 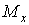, і 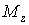діють ще поперечні сили й . Найбільші дотичні напруження від цих сил будуть відповідно в точках K і L:

у точці K

у точці L

Небезпечну точку перетину знайдемо, визначивши положення нейтральної лінії. Остання перпендикулярна до площини дії результуючого згинального моменту

Напрямок нейтральної лінії легко визначити графічно (рис. 17), тому що воно збігається з напрямком вектора .

Рис. 17. Графічне визначення напрямку нейтральної лінії

Небезпечною точкою в перетину є точка S (рис. 15). Природно, що в цій точці дотичні напруження й будуть значно менше обчислених вище максимальних значень. Приймемо приблизно й з деяким запасом, що в небезпечній точці і S до дотичних напружень 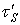від крутного моменту М_к:

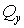додається наступне дотичне напруження від поперечних сил і :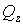

Обчислимо еквівалентну напругу в точці S по IV теорії:

Еквівалентне напруження в тій же точці без врахування впливу, поперечних сил

Отже, якщо врахувати дію поперечних сил, то напруження збільшаться на

У небезпечному перерізі щоки (рис. 16) діє тільки поперечна сила ; поперечна сила . Поперечна сила 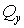не дає дотичних напружень у найнебезпечнішій точці перетину L. Тому розглянемо її вплив у точці , де викликані нею дотичні напруження досягають найбільшої величини:

і збігаються по напрямку з дотичними напруженнями від впливу крутного моменту . Величина останніх

Обчислимо еквівалентне напруження по IV теорії міцності:

У тій же точці напруження без урахування 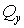вже обчислені:

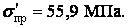
Таким чином, поперечні сили збільшують напруження в точці на

Якщо в перетині діє осьова сила, згинальні моменти в головних площинах і крутний момент, то умова міцності, наприклад, по IV теорії, у точці K(рис. 16) має вигляд

(25)

Аналогічно в крапці S

(26)

У розглянутому небезпечному перерізі щоки діє поздовжня сила, що розтягує. Викликане нею нормальне напруження, що розтягує

настільки мало, що їм можна зневажити.

Питання для самоконтролю

1. Як визначити небезпечний переріз вала при згині з крученням? Який напружений стан виникає в поперечному перерізі?

2. Розкрийте, сутність проектного і перевірного розрахунків на міцність вала при згині з крученням