
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вплив умов закріплення кінців стрижня на величину критичної сили
Вище розглянуто так званий основний випадок навантаження і закріплення кінців стиснутого стрижня — стрижня із шарнірно обпертими кінцями. Як було показано, після втрати стійкості на довжині стрижня укладається тільки одна напівхвиля  .
.
Розглянемо інші випадки закріплення кінців стрижня:
1. Стрижень довжиною  жорстко затиснений одним кінцем і стиснутий поздовжньою силою, прикладеною до вільного кінця (рис. 5,а).
жорстко затиснений одним кінцем і стиснутий поздовжньою силою, прикладеною до вільного кінця (рис. 5,а).

| |
| а | б |
Рис. 5. Стрижень, жорстко затиснений одним кінцем
Порівнюючи рис. 14.5, а й б, бачимо, що вигнута вісь стрижня, жорстко затиснутого одним кінцем, перебуває в таких же умовах, як і верхня половина стрижня довжиною  із шарнірно закріпленими кінцями. Таким чином, критична сила для стрижня з одним затиснутим, а іншим вільним кінцем така ж, як і для стрижня із шарнірно обпертими кінцями при довжині
із шарнірно закріпленими кінцями. Таким чином, критична сила для стрижня з одним затиснутим, а іншим вільним кінцем така ж, як і для стрижня із шарнірно обпертими кінцями при довжині 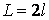 , тобто
, тобто

| (17) |
При цьому вигнута вісь стрижня (рис. 14.5, а) має вигляд половини напівхвилі синусоїди.
2. Стрижень довжиною  , у якого обидва кінці жорстко затиснені (рис.6). Після втрати стійкості стрижня внаслідок симетрії середня його частина довжиною
, у якого обидва кінці жорстко затиснені (рис.6). Після втрати стійкості стрижня внаслідок симетрії середня його частина довжиною  працює в тих же умовах, що й стрижень при шарнірно обпертих кінцях. При цьому утворяться дві напівхвилі: середня, довжиною
працює в тих же умовах, що й стрижень при шарнірно обпертих кінцях. При цьому утворяться дві напівхвилі: середня, довжиною  , і дві крайні половинки напівхвилі довжиною
, і дві крайні половинки напівхвилі довжиною  .
.

Рис. 6. Стрижень, у якого обидва кінці жорстко затиснені
Критичну силу в цьому випадку знаходимо з рівняння (14) при  :
:

| (18) |
3. Стрижень довжиною  забитий одним кінцем і шарнірно обпертий на іншому (рис. 7). Після втрати стійкості права частина
забитий одним кінцем і шарнірно обпертий на іншому (рис. 7). Після втрати стійкості права частина  стрижня має вигляд напівхвилі синусоїди. З порівняння рис. 7 і 5, б знаходимо, що ділянка
стрижня має вигляд напівхвилі синусоїди. З порівняння рис. 7 і 5, б знаходимо, що ділянка  довжиною
довжиною  перебуває в таких же умовах, як і стрижень із шарнірно закріпленими кінцями. Виходить,
перебуває в таких же умовах, як і стрижень із шарнірно закріпленими кінцями. Виходить,

| (19) |

Рис. 7. Стрижень, затиснений одним кінцем і шарнірно обпертий іншим
Співвідношення (14), (17) – (19) можна об'єднати в одну формулу
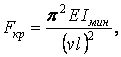
| (20) |
де  — наведена довжина стрижня;
— наведена довжина стрижня;  — фактична довжина стрижня;
— фактична довжина стрижня;
 — коефіцієнт приведення довжини.
— коефіцієнт приведення довжини.
Таким чином, різні випадки обпирання й навантаження стрижня приводяться до основного випадку введенням у формулу наведеної довжини  . Це поняття вперше було уведено Ф. С. Ясинським.
. Це поняття вперше було уведено Ф. С. Ясинським.
З формули Ейлера (20) видно, що критичне навантаження залежить від найменшої жорсткості  , довжини стрижня
, довжини стрижня  й коефіцієнта
й коефіцієнта  .
.

Рис. 8. Значення коефіцієнтів приведення довжини
Дата добавления: 2015-02-09; просмотров: 896; Мы поможем в написании вашей работы!; Нарушение авторских прав |