Магнитный момент контура с током. Вращающий момент.

Для исследования магнитного поля применяется плоский замкнутый контур с током очень малых размеров. Будем называть такой контур пробным контуром. Ориентацию его в пространстве характеризует направление нормали к контуру, восстанавливаемой по правилу правого винта (буравчика): если вращать рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали.

Магнитное поле контура характеризуется магнитным моментом

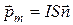, (12)

где I – сила тока в контуре, S - площадь контура, направление магнитного момента совпадает с направлением нормали . В СИ единица измерения магнитного момента - .

Рис. 9

Помещая пробный контур в магнитное поле, обнаружим, что на грани контура действуют силы Ампера. Причем пара сил и , действующих на противоположные грани (рис. 10) направлены таким образом, что стремятся повернуть контур в определенном направлении.

Рис. 10

Возникает вращающий момент 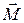, зависящий как от свойств магнитного поля в данной точке, так и от свойств контура. Вращающий момент определяется векторным произведением магнитного момента на вектор индукции магнитного поля

(13)

Вращающий момент – псевдовектор, направленный вдоль оси вращения таким образом, что с его острия виден переход от вектора магнитного момента к вектору индукции магнитного поля против часовой стрелки. Скалярное значение вращающего момента , где α – угол между и 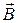. При α=90° вращающий момент принимает максимальное значение . При α=0° или α=180° вращающий момент М=0. Таким образом, вращение контура будет происходить до тех пор, пока вектора магнитного момента и индукции магнитного поля не совпадут.

Вращение контура с током в магнитном поле используется не только для обнаружения магнитного поля, но и лежит в основе принципа действия электродвигателей и электроизмерительных приборах магнитоэлектрической системы

Электродвигатель постоянного тока преобразует электрическую энергию в механическую. Пусть рамка с током находится в магнитном поле постоянного магнита в положении, когда угол между вектором магнитного момента и вектором магнитной индукции 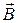равен 180° (неустойчивое равновесие), поворачивается на 180⁰ вокруг горизонтальной оси. В момент, когда рамка проходит положение устойчивого равновесия (угол между вектором магнитного момента и вектором магнитной индукции 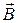равен 0⁰), коллектор изменяет направление тока в рамке на противоположное. В результате рамка вновь оказывается в положении неустойчивого равновесия и, пройдя по инерции это положение, продолжает вращение в прежнем направлении.

Рис. 11

Пример 9. Квадратная проволочная рамка со стороной а=10 см помещена в однородное магнитное поле с индукцией В=1 Тл. Сила тока в рамке I=50 А. Определить потенциальную (механическую) энергию рамки в магнитном поле, если на рамку действует механический момент М=0,25 Н·м.

Дано: а=10 см=0,1 м, В=1 Тл, I=50 А, М=0,25 Н·м

Решение: На контур с током в магнитном поле действует вращающий момент: , где - модуль магнитного момента рамки, - площадь рамки, I – сила тока в рамке, В – индукция магнитного поля, α- угол между вектором магнитного момента и вектором магнитной индукции.

При повороте рамки совершается элементарная механическая работа . Полную работу найдем путем интегрирования .

Механическая работа равна изменению потенциальной энергии, взятой со знаком «-»: . Из сопоставления формул имеем формулу для потенциальной энергии контура с током в магнитном поле .

Так как , а , тогда .

Вычисления:

.