Движение заряженной частицы в магнитном поле.

Сила Ампера, действующая на элемент проводника 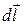с током I, находящийся в магнитном поле 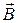, может быть выражена через силы, действующие на отдельные носители заряда. Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя, –скорость упорядоченного движения носителей по проводнику, S – площадь поперечного сечения проводника, dN – число носителей заряда в проводнике 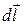. Сила тока в проводнике .Сила, действующая на одну частицу:

,

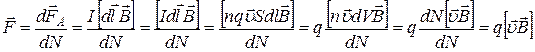где , 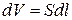- объем проводника.

Эту силу называют силой Лоренца. То есть сила Лоренца – сила, действующая на движущуюся в магнитном поле заряженную частицу.

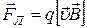(14)

Направление силы Лоренца определяют по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, а четыре вытянутых пальца показывали направление скорости положительно заряженной частицы или противоположное направление скорости отрицательно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца.

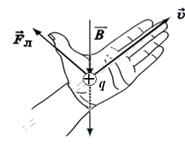
Рис. 11

Модуль силы Лоренца определяется по формуле

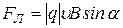, (15)

где α – угол между векторами скорости частицы и индукции магнитного поля, угол влета заряженной частицы в магнитное поле.

Сила Лоренца перпендикулярна скорости частицы, поэтому при движении заряженной частицы в магнитном поле сила Лоренца работы не совершает, а модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору магнитной индукции, то частица будет двигаться по окружности радиуса R (рис. 12). Сила Лоренца в этом случае играет роль центростремительной силы.

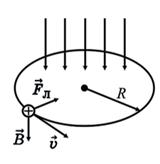
Рис. 12

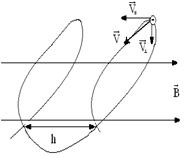
Если заряженная частица влетает в однородном магнитном поле под углом α, то частица будет двигаться по спирали радиуса R и шагом h (шаг спирали – это расстояние, на которое смещается электрон вдоль силовой линии магнитного поля за время, равное периоду). Движение заряженной частицы в этом случае можно разложить на движение по инерции вдоль силовых линий 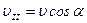со скоростью и по окружности под действием силы Лоренца со скоростью .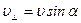

Пример 10. Протон (масса протона m_p=1,67·10^-27кг, заряд протона q_p=1,6·10^-19Кл), пройдя в электрическом поле ускоряющую разность потенциалов Δφ=100 кВ, влетел в однородное магнитное поле с индукцией В=5 Тл перпендикулярно линиям индукции начал двигаться по окружности. Определить частоту вращения протона.

Дано: m_p=1,67·10^{-27 кг}, q_p=1,6·10^-19 Кл, Δφ=100 кВ=10⁵ В, В=5 Тл, a=90⁰

Решение:

На заряженную частицу в магнитном поле действует сила Лоренца, равная , где q- заряд частицы, q=1,6×10^-19 Кл, υ - скорость частицы, a- угол между векторами скорости и магнитной индукцией, a=90⁰, так как скорость перпендикулярна вектору магнитной индукции.

Сила Лоренца является центростремительной, то есть 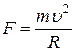, где R- радиус окружности, по которой движется частица, m –масса частицы, для протона m=1,67×10^-27кг. Получаем соотношение , отсюда радиус окружности равен .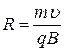

Период обращения заряженной частицы . Выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.

Частота обращения частицы – это число оборотов в единицу времени, величина, обратная периоду, тогда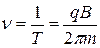

Вычисление: (Гц)

Пример 11. Электрон, масса которого m_е=9,11·10^-31кг, а заряд электрона q_е=1,6·10^-19 Кл, влетел в однородное магнитное поле под углом α=60˚ к направлению линий магнитной индукции и движется по спирали радиуса R=2 см. индукция магнитного поля В=10 мТл. Определить шаг спирали, по которой движется электрон.

Дано: m_е=9,11·10^-31кг, q_е=1,6·10^-19 Кл, α=60˚, R=2 см=0,02 м, В=10 мТл=0,01 Тл

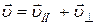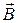Решение: Разложим скорость движения электрона на две составляющие: , где -составляющая, параллельная вектору магнитной индукции , -составляющая, перпендикулярная вектору магнитной индукции .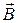

Движение электрона в магнитном поле сложное: по инерции вдоль силовых линий со скоростью и по окружности под действием силы Лоренца со скоростью . Результатом сложения этих двух движений является движение по спирали.

Сила Лоренца при этом равна ,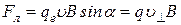

где q_е – заряд электрона, В – индукция магнитного поля, в котором движется электрон.

Сила Лоренца является центростремительной, поэтому , где m_е – масса электрона, R – радиус спирали, по которой движется электрон. Так как , то радиус спирали .

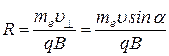Период вращения электрона равен .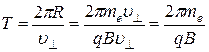

Шаг спирали – это расстояние, на которое смещается электрон вдоль силовой линии магнитного поля за время, равное периоду

.

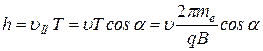Тогда , получаем .

Вычисление: .