Электромагнитная индукция.

В 1831 году М.Фарадей открыл явление электромагнитной индукции, которое заключается в возникновении электрического тока в проводящем контуре, при изменении магнитного потока, пронизывающего этот контур. Возникающий ток называется индукционным (индукция – (с лат.) наведение). Закон электромагнитной индукции (закон Фарадея):ЭДС электромагнитной индукции в замкнутом контуре равна скорости изменения магнитного потока через поверхность, ограниченную этим контуром.

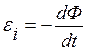(33)

Если контур содержит N витков, то ЭДС индукции равна скорости изменения потокосцепления,

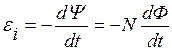(34)

Знак «минус» в формулах 15 и 16 является математическим выражением правила Ленца, согласно которому, индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.

Рис. 16

Направление индукционного тока определяется следующим образом: установить направление внешнего магнитного поля В, определить увеличивается или уменьшается поток вектора магнитной индукции внешнего поля, по правилу Ленца указать направление вектора магнитной индукции индукционного тока В_i., по правилу правого винта определить направление индукционного тока в контуре. На рис. 15 виток проводника помещен в неоднородное магнитное поле, созданное движущимся постоянным магнитом, так как индукция внешнего магнитного тока В нарастает, то вектора 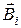и 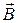антипараллельны.

Согласно гипотезе Максвелла, природа ЭДС индукции заключается в возникновении вихревого электрического поля в любой области пространства, где существует переменное магнитное поле.

Возникновение ЭДС индукции в движущемся проводнике объясняется действием силы Лоренца со стороны магнитного поля на движущиеся вместе с проводником электрические заряды. Пусть проводник длиной l перемещается со скоростью в однородном магнитном поле с индукцией 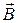, то ЭДС индукции, возникающая в проводнике равна

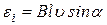(35)

где α – угол между вектором магнитной индукции и скоростью движения проводника.

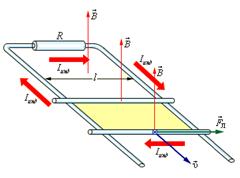
Рис. 17

Самоиндукция – это явление возникновения индукционного тока в замкнутом контуре при изменении силы тока в нем (частный случай электромагнитной индукции).

При протекании в контуре тока I создается магнитное поле, характеризующееся магнитным потоком Ф.

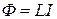, (36)

где L - коэффициент самоиндукции или индуктивность контура, которая зависит от геометрической формы контура, его размеров и от среды, в которой он находится. Единицы измерения индуктивности в СИ Генри .

ЭДС самоиндукции пропорциональна скорости изменения силы тока в контуре.

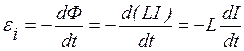(37)

Для катушки имеем

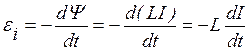, (38)

где L - коэффициент самоиндукции или индуктивность катушки, которая как и индуктивность контура зависит от геометрической формы контура, его размеров и от среды, в которой он находится. Индуктивность катушки определяется как коэффициент пропорциональности между потокосцеплением и силой тока в катушке: 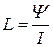. С учетом формулы (22) получим индуктивность соленоида при отсутствии сердечника: ,

а при наличии сердечника с магнитной проницаемостью μ:

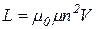(39)

где μ₀ – магнитная постоянная, – число витков, приходящееся на единицу длины соленоида, 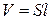- объем соленоида, S – площадь сечения.

В электрической цепи, содержащей индуктивность, при размыкании цепи сила тока изменяется по закону

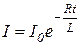, (40)

А при замыкании цепи сила тока изменяется по закону

, (41)

где I₀ - максимальная сила тока, R - сопротивление цепи, L - индуктивность катушки, t - время процесса.

Если два контура расположены один возле другого и в каждом из них изменяется сила тока, то они будут взаимно влиять друг на друга. Изменение в первом контуре вызовет появление индуцированной ЭДС во втором контуре и, наоборот, изменение тока и магнитного поля второго контура будет причиной появления индуцированной ЭДС в первом контуре. Это явление называется взаимоиндукцией, а ЭДС, возникающая вследствие влияния контуров друг на друга, называется ЭДС взаимоиндукции

, (42)

где L - коэффициент взаимной индукции.

Явление электромагнитной индукции лежит в основе принципа действия многих инженерных устройств, таких как генератор переменного тока, трансформатор, поезд на магнитной подушке, детекторы металлов и так далее.

Генератор переменного тока - устройство, преобразующее механическую энергию в электрическую энергию. В настоящее время имеется много типов индукционных генераторов, но все они состоят из одних и тех же основных частей. Это, во-первых, электромагнит или постоянный магнит, создающий магнитное поле, и, во-вторых, обмотка или рамка, в которой индуцируется переменная ЭДС. В некоторых генераторах (рис. 18 а) обмотка вращается вокруг горизонтальной или вертикальной оси. Поэтому он называется ротором. Неподвижный электромагнит называют статором. При этом угол между вектором индукции магнитного поля, созданного электромагнитом или постоянным магнитом, изменяется по закону 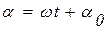, где -циклическая частота, 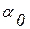- начальная фаза вращения. Согласно закону Фарадея ЭДС индукции равна скорости изменения полного магнитного потока 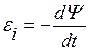. 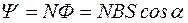- полный магнитный поток, пронизывающий обмотку, состоящую из N витков. Тогда .

В больших промышленных генераторах (рис. 18 б) вращается электромагнит, который является ротором, в то время как обмотки, в которых наводится ЭДС, уложены в пазах статора и остаются неподвижными. Дело в том, что подводить ток к ротору или отводить его из обмотки ротора во внешнюю цепь приходиться при помощи скользящих контактов. Для этого ротор снабжается контактными кольцами, присоединенными к концам его обмотки. Неподвижные пластины - щетки - прижаты к кольцам и осуществляют связь обмотки ротора с внешней цепью.

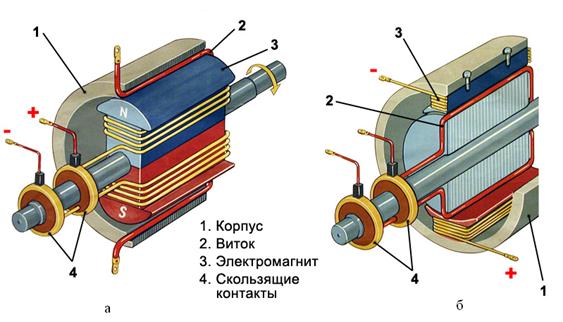
Рис. 18

Пример 15: В однородном магнитном поле, индукция которого В=0,1Тл, вращается катушка, состоящая из N=200 витков. Ось вращения катушки перпендикулярна к ее оси и к направлению магнитного поля. Период обращения катушки Т=0,2 с; площадь поперечного сечения S=4 см². Найти максимальную ЭДС индукции ε_max во вращающейся катушке.

Дано: В=0,1 Тл, N=200, Т=0,2 с, S=4 см²=4·10^{-4 м2}.

Решение: Согласно закону Фарадея ЭДС индукции равна скорости изменения магнитного потока . - полный магнитный поток, пронизывающий катушку (потокосцепление), где 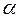- угол между векторами магнитной индукции и нормалью, проведенной к контуру, при вращении рамки в магнитном поле угол изменяется по формуле 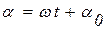, 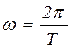-циклическая частота, 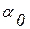- начальная фаза вращения.

Тогда 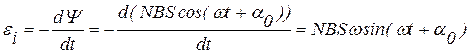, максимальная ЭДС равна .

Вычисления: .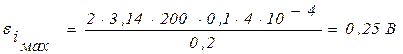

Пример 16. Плоский проводящий контур с площадью S=50 см² помещен в однородное магнитное поле, индукция которого В=4 мТл. Сопротивление контура R=1 Ом. Плоскость контура составляет угол α=30˚ с линиями магнитной индукции. Определить величину заряда q, который пройдет по контуру при выключении магнитного поля.

Дано: S=50 см²=5·10^{-3 м², В=}4 мТл=0,004 Тл, R=1 Ом, α=30˚.

Решение: Согласно определению сила тока равна величине заряда переносимого через данную площадь сечения в единицу времени, то есть 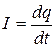. Согласно закону Ома сила тока равна . Согласно закону Фарадея ЭДС индукции равна скорости изменения магнитного потока 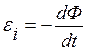. Тогда получаем соотношение 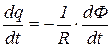или 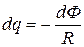. Чтобы найти искомое количество заряда проинтегрируем последнее выражение .

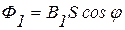- магнитный поток, пронизывающий контур при включенном поле, где- угол между векторами магнитной индукции и нормалью, проведенной к контуру, .

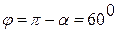- магнитный поток, пронизывающий контур при выключенном поле, так как 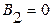, то .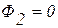

Искомое значение заряда .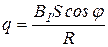

Вычисляем Кл.

Пример 17. Горизонтальный стержень длиной l=1 м вращается вокруг вертикальной оси, проходящей через один из его концов. Ось вращения параллельно магнитному полю, индукция которого В=50 мкТл. При какой частоте вращения ν стержня разность потенциалов на концах этого стержня U=1 мВ?

Дано: l=1 м, В=50 мкТл=5·10^-5 Тл, U=1 мВ=10^-3 В

Решение: Разность потенциалов возникает за счет наведения в проводнике ЭДС индукции 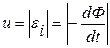, где Ф – магнитный поток, пересекаемый проводником при движении, 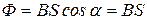, α=0, так как плоскости вращения, тогда .

При вращении площадь, пересекаемая проводником пропорциональна углу поворота 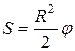, где - радиус описываемой окружности.

Получаем , так как 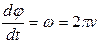- угловая скорость, то получаем .

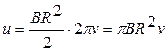Искомая частота вращения .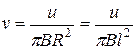

Вычисление: 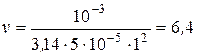(Гц)

Пример 18. По соленоиду, содержащему N=600 витков, течет ток силой I=5 А. Длина соленоида l=40 см, площадь его сечения S=10 см², сердечник немагнитный. Определить среднее значение ЭДС ε_sср самоиндукции, которая возникает в соленоиде, если сила тока уменьшается практически до нуля за время Δt=0,4 мс после отключения соленоида от источника тока.

Дано: N=600, I₀=5 А, I=0 А, l=40 см=0,4 м, S=10 см²=10^-3м², Δt=0,4 мс=4·10^-4с

Решение: ЭДС самоиндукции определяется по формуле , где 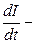скорость изменения силы тока в соленоиде.

Среднее значение ЭДС самоиндукции ,

где 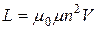- индуктивность соленоида, где μ₀=1,26·10^-6 Гн/м – магнитная постоянная, μ – магнитная проницаемость среды, так как сердечник немагнитный μ=1, – число витков, приходящееся на единицу длины, - объем соленоида. Тогда .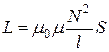

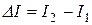- изменение силы ток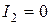а 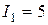( А, А)

Получаем .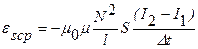

Вычисления: .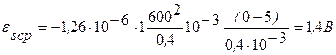

Пример 19: Источник тока замкнут на катушку с индуктивностью L=0,4 Гн. Определить сопротивление R катушки, если сила I тока в катушке достигает 20 % ее максимального значения за время t=0,1 с после замыкания цепи.

Дано: L=0,4 Гн, I=0,2I₀, t=0,1 с.

Решение: При замыкании цепи сила тока определяется по формуле

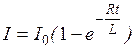, где , тогда 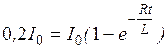или 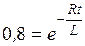, получаем 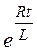=1,25или .

Искомое сопротивление .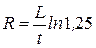

Вычисление: 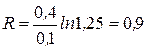Ом.