Магнитный поток. Работа в магнитном поле по перемещению проводника и контура с током в магнитном поле.

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS, которую можно считать плоской и в пределах которой магнитное поле можно считать однородным, называется физическая величина, равная скалярному произведению вектора магнитной индукции 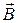и вектора площади 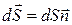, модуль которого равен dS, а направление совпадает с направлением нормали к площадки

, (18)

где α – угол между векторами магнитной индукции 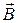и нормали .

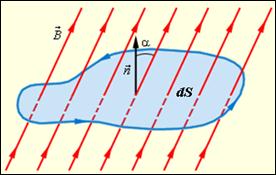
Рис. 14

Поток вектора магнитной индукции через произвольную поверхность S равен

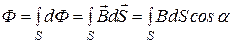. (19)

Для однородного магнитного поля и плоской поверхности площадью S магнитный поток определяется по формуле:

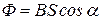, (20)

Единица измерения магнитного потока вебер: .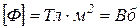

Следствием вихревого характера магнитного поля и замкнутости силовых линий магнитной индукции является выражение:

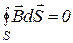. (21)

Формула (21) является математическим выражением теоремы Гаусса для потока вектора магнитной индукции: Магнитный поток сквозь произвольную замкнутую поверхность равен нулю.

В качестве примера рассчитаем магнитный поток через соленоид в вакууме. Магнитный поток через один виток соленоида площадью S равен

,

учтем, что виток соленоида расположен перпендикулярно вектору магнитной индукции 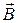, то есть угол между вектором магнитной индукции и нормалью равен 0.

Полный магнитный поток в вакууме, сцепленный со всеми витками катушки, называемый потокосцеплением, равен 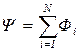. Для соленоида имеем

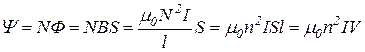, (22)

где - число витков, приходящихся на единицу длины, 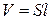- объем соленоида.

Работа по перемещению проводника с током в магнитном поле связана с магнитным потоком, который пересекает проводник при движении в магнитном поле. При перемещении проводника произвольной формы с током I работа определяется формулой

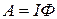, (23)

где Ф – магнитный поток, пересекаемый проводником при движении.

Работа по перемещению контура с током в магнитном поле связана с изменением магнитного потока, сцепленного с контуром. При перемещении контура произвольной формы с током I работа определяется формулой

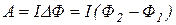, (24)

где Ф₁ – магнитный поток, пронизывающий контур в начальном положении до перемещения, Ф₂ – магнитный поток, пронизывающий контур в конечном положении после перемещения.

Пример 13. Тонкое проводящее кольцо радиусом R=20 см подвешено свободно в однородном магнитном поле с индукцией В=0,1 Тл. Сила тока в кольце I=2 А. Какую работу надо совершить, чтобы повернуть кольцо на угол φ=60˚ вокруг оси, лежащей в плоскости кольца и проходящей через его центр?

Дано: R=20 см=0,2 м, В=0,1 Тл, I=2 А, φ=60˚

Решение:

Работа при перемещении рамки с током в магнитном поле равна , где I- сила тока в рамке, DФ – изменение магнитного потока, DФ=Ф₂-Ф₁.

Магнитный поток определяется по формуле 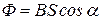, α - угол между вектором магнитной индукции и нормалью, проведенной к контуру; S– площадь рамки, S=pR².

Тогда 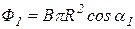, где a₁=0⁰ – рамка свободно установилась в магнитном поле; 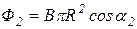, где a₂=a₁+j=60⁰.

Искомая работа равна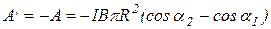

Найдем численное значение

А^/=-1,26×10^-6×2×10⁵×3,14×0,2²(cos60⁰- cos0⁰)=0,016 Дж.