Случайные величины. Случайной называется величина, которая в результате испытания принимает одно и только одно возможное значение

Случайной называется величина, которая в результате испытания принимает одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин. Дискретнойназывается такая случайная величина, значения которой есть счетное множество фиксированных величин. Непрерывной называют такую случайную величину, которая принимает любое значение из некоторого интервала. Случайные величины обозначаются прописными буквами Х, У, Z, а их возможные значения соответствующими малыми буквами.

Для описания поведения дискретной случайной величины Х задают все значения , которые она может принять, и вероятности появления этих значений ( ).

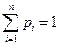Законом распределения вероятностей (рядом распределения) дискретной случайной величины называется последовательность возможных значений случайной величины и соответствующих им вероятностей, представленная в виде таблицы:

Х			…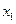
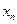
р			…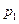

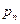
Математическим ожиданием дискретной случайной величины называется сумма вида 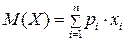. Математическое ожидание характеризует среднее значение случайной величины.

Рассеяние случайной величины около среднего значения характеризует дисперсия. Дисперсией дискретной случайной величины Х является:

.

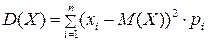Непрерывные случайные величины характеризуются тем, что их значения могут сколь угодно мало отличаться друг от друга.

Вероятность события 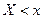(где Х – значение непрерывной случайной величины, а x – произвольно задаваемое значение), рассматриваемая как функция от x, называется функцией распределения вероятностей: .

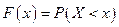Производная от функции распределения вероятностей называется функцией плотности распределения вероятностей или плотностью вероятности: .

Математическим ожиданием непрерывной случайной величины называется значение интеграла . Дисперсией непрерывной случайной величины называется значение интеграла .