Точечные оценки

Оценки параметров генеральной совокупности, полученные на осно­вании выборки, называются статистическими. Если статистическая оценка характеризуется одним числом, она называется точечной. К чис­лу таких оценок относятся выборочная средняя и выборочная диспер­сия.

Выборочная средняяопределяется как среднее арифметическое по­лученных по выборке значений:

,

где – варианта выборки; – частота варианты; – объем выборки.

Выборочная дисперсияпредставляет собой среднюю арифметическую квадратов отклонений вариант от их выборочной средней: .

Статистическая оценка является случайной величиной и меняется в зависимости от выборки. Если математическое ожидание статистиче­ской оценки равно оцениваемому параметру генеральной совокупности, то такая оценка называется несмещенной,если не равно – то смещен­ной.

Выборочная средняя является оценкой математического ожидания случайной величины и представляет собой несмещенную оценку. Выбо­рочная дисперсия оценивает дисперсию генеральной совокупности и яв­ляется смещенной оценкой.

Для устранения смещенности выборочной дисперсии ее умножают на величину 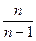и получают 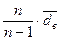. Величину называют несмещеннойили «исправленной» выборочной дисперсией.