
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условная вероятность. Теорема умножения. Независимость событий
Определение. Условной вероятностью события А по отношению к событию В называется вероятность события А при условии, что событие В произошло. Обозначается P(A/B).
Определение. События А и В независимы, если P(A/B)=P(A).
Теорема 3. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий, т.е. P(AB)=P(A)·P(B).
Теорема 4. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго: P(AB)=P(A)·P(B/A) =P(В)·P(A/B).
Примеры:
1. Два стрелка независимо друг от друга делают по одному выстрелу в цель. Известно, что вероятность попадания р1 первого стрелка равна 0,9, а вероятность попадания р2 второго – 0,8. Найти вероятность того, оба стрелка попадут в цель.
Решение.
Рассмотрим событие: А=«попадание первого стрелка в цель», В=«попадание второго стрелка в цель». Тогда событие АВ=«оба стрелка попали в цель». Так как события А и В независимы по условию, то
Р(АВ)=Р(А)Р(В)=р1р2 = 0,72.
Ответ: 0,72.
2. В урне имеется 3 красных и 7 белых шаров. Вынимают сначала один шар и, не возвращая его в урну, второй. Какова вероятность того, что оба шара белые?
Решение.
Пусть событие А=«первый шар белый», В=«второй шар белый». Тогда событие АВ=«оба шара белые».
Р(АВ)=Р(А) Р(В/А).
 . Условная вероятность P(В/А) того, что второй шар белый, вычисляется при условии, что уже вынут один белый шар, следовательно,
. Условная вероятность P(В/А) того, что второй шар белый, вычисляется при условии, что уже вынут один белый шар, следовательно,  . Итак,
. Итак,  .
.
Ответ. 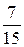 .
.
Дата добавления: 2015-02-10; просмотров: 299; Мы поможем в написании вашей работы!; Нарушение авторских прав |