Формула полной вероятности. Формула Байеса

Теорема. Пусть события Н₁, Н₂, ... ,Н_n образуют полную группу попарно несовместных событий. И пусть событие А может произойти с каждым из этих событий, тогда

Р(А)=Р(Н₁)Р(А/H₁)+P(H₂)P(A/H₂)+ ... + P(H_n)P(A/H_n). (1)

Замечание. События Н₁, Н₂, ... ,Н_n называются гипотезами. Формула (1) – формулой полной вероятности.

Пример:

Имеется 2 одинаковых ящика с деталями. В первом ящике имеется 10 деталей, из них 2 нестандартных, во втором ящике тоже 10 деталей, из них 1 нестандартная. Из одного наугад выбранного ящика вынимается 1 деталь. Какова вероятность, что эта деталь стандартная?

Решение.

Пусть событие А=«взятая деталь стандартная».

Введем события (гипотезы): Н₁=«выбран первый ящик», Н₂=«выбран второй ящик».

Тогда событие А можно представить в виде А=Н₁А + Н₂А, отсюда Р(А)=Р(Н₁)Р(А/H₁)+P(H₂)P(A/H₂).

Ящиков два, следовательно, Р(Н₁)=Р(Н₂)= . Так как в первом ящике всего 10 деталей, из них 8 стандартных, то P(A/H₁) = = 0,8; аналогично

P(A/H₂) = = 0,9.

Итак, по формуле полной вероятности получаем:

Р (А)= 0,5× 0,8 + 0,5 × 0,9 = 0,85.

Ответ. 0,85.

Допустим, что испытание проведено, и в результате этого испытания событие А произошло. Вероятности каждой гипотезы при условии, что событие А произошло, вычисляются по формулам:

, .

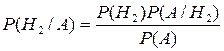Эти формулы позволяет переоценить вероятность каждой гипотезы после того, как становится известным, что в результате испытания произошло событие А. Следовательно, в общем виде получаем

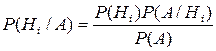. (2)

Формула (2) называется формулой Байеса.

Пример:

Пусть выполнены условия предыдущего примера и пусть испытание произведено и оказалось, что вынутая деталь стандартная. Найти вероятность того, что она извлечена из первого ящика.

Решение.

Введем те же обозначения для событий, что и при решении предыдущего примера. Требуется найти Р(A/H₁). Так как Р(Н₁) = 0,5, Р(А/Н₁) = 0,8, Р(А) = 0,85, то по формуле (2) имеем

.

Ответ. 0,47.

Как видно, до испытания Р(Н₁) = 0,5, а после того как стал известен результат испытания (вынута стандартная деталь), вероятность гипотезы Н₁ изменилась, что вполне согласуется со здравым смыслом, так как в первом ящике стандартных деталей было меньше.