Схема упорядоченных размещений

Пусть множество состоит из п элементов: п₁ – элементы первого рода, п₂ – элементы второго рода, …, п_k – k-го рода, причем п₁ + п₂ +…+ п_k = п. Число способов разбиения множества на k упорядоченных частей и число перестановок п из элементов множества обозначается и вычисляется по формуле

.

Примеры:

1. В турнире участвуют 6 человек. Сколькими способами могут распределиться между ними места?

Решение.

Так как каждый человек займет какое-либо место с 1 по 6-е, следовательно, будем использовать формулу перестановок:

Р₆ = 6! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720.

Ответ. 720 способов.

2. Сколькими способами может быть присуждены 1, 2 и 3 премии трем лицам, если число соревнующихся 12?

Решение.

Так как порядок выбора элементов важен, следовательно, для подсчета способов будем использовать формулу размещений без повторений (т.к. один и тот же человек не может занять, например, 2 и 3 места одновременно). Получаем:

.

Ответ: 1320 способов.

3. Сколькими способами читатель может выбрать 4 книги из 6?

Решение.

Так как порядок выбора элементов не важен (т.е. книги можно взять в произвольном порядке), следовательно, для подсчета способов будем использовать формулу сочетаний без повторений. Получаем:

.

Ответ: 15 способов.

4. Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил «неуд».

Решение.

Каждый из студентов может получить любую из отметок: «удовлетворительно», «хорошо», «отлично». Причем отметки могут повторяться. И так как важно, какую отметку получит каждый из студентов, то, следовательно, для подсчета способов будем использовать формулу размещений с повторениями. Получаем:

.

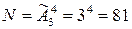Ответ: 81 способ.

5. Сколько различных «слов» (необязательно осмысленных) можно получить, переставляя буквы в слове: а) СОЛНЦЕ; б) MISSISSIPPI?

Решение.

а) В слове СОЛНЦЕ нет повторяющихся букв, новые «слова» получаются перестановкой букв, следовательно, для подсчета количества новых «слов» будем использовать формулу перестановок. Так как букв в исходном слове 6, получим:

.

б) В слове MISSISSIPPI есть повторяющиеся буквы. Разобьем данное множество на подмножества. Пусть буквы М – элементы 1-го рода, тогда

п₁ = 1; буквы I – элементы 2-го рода, тогда п₂ = 4; буквы S – элементы 3-го рода, п₃ = 4; буквы Р – элементы 4-го рода, п₄ = 2. Всего букв в слове 11, т.е. п = 11. Для подсчета будем использовать схему упорядоченных размещений, получим:

.

Ответ: а) 720 способов; б) 34650 способов.

6. В почтовом отделении продаются открытки 6 видов. Покупатель выбил чек на 4 открытки. Считая, что любой набор товаров равновозможен, определить число возможных вариантов покупки.

Решение.

Порядок выбора открыток не важен и так как не сказано, что открытки должны быть разного вида, то для подсчета способов будем использовать формулу сочетаний с повторениями. Получим:

.

Ответ: 126 способов.