Законы операций над множествами

Для любых подмножеств А, B и C универсального множества I справедливы следующие тождества:

1. , ;

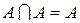2. , ;

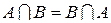3. , ;

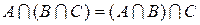4. , ;

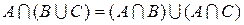5. , ;

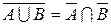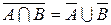6. ;

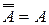7. , .

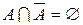Примеры:

1. Доказать тождество .

Доказательство:

Докажем аналитически. Преобразуем левую часть равенства, используя законы операций над множествами:

.

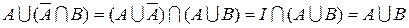После преобразований получили правую часть. Следовательно, тождество верно.

Докажем графически. Изобразим левую и правую часть на кругах Эйлера.

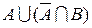
Так как залитые темно-серым цветом области на первой и второй схеме совпадают, следовательно, делаем вывод, что тождество верно.

2. Доказать тождество .

Докажем данное тождество графически. Рассмотрим левую часть равенства:

Серым цветом на схеме показано действие, выполняемое в скобках 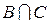, а штриховкой – результат выполнения действий в левой части равенства, т.е. 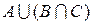. Обведем жирной линией результат действий над множествами.

Теперь рассмотрим правую часть равенства:

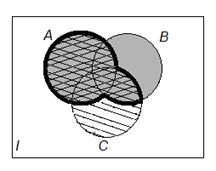
Серым цветом на схеме показано выполнение действия в первой скобке , штриховкой с наклоном влево – результат действия во второй скобке 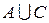, штриховкой с наклоном вправо – результат пересечения первой и второй скобки. Обведем жирной линией область, где пересекаются штриховые линии, это и будет результат выполнения действий в правой части.

Так как области, обведенные жирной линией в левой и правой части совпадают, следовательно, делаем вывод, что данное тождество верно.