Метод математической индукции

В основе всякого математического исследования лежат дедуктивный или индуктивный методы. Дедуктивный метод рассуждений - это рассуждение от общего к частному, т.е. рассуждение, исходным моментом которого является общий результат, а заключительным моментом – частный результат. Индукция применяется при переходе от частных результатов к общим, т.е. является методом, противоположным дедуктивному.

По своему первоначальному смыслу слово «индукция» применяется к рассуждениям, при помощи которых получают общие выводы, опираясь на ряд частных утверждений.

Рассмотрим доказательство методом математической индукции на примере.

Доказать, что для любого натурального n, справедливо равенство:

.

Доказательство.

1) Пусть n=1, тогда 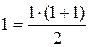. Следовательно, утверждение верно при n=1.

2) Докажем, что данное равенство справедливо для (k+1).

Пусть k – любое натуральное число и пусть утверждение справедливо для n=k, т.е. .

Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, т.е. что .

Действительно,

.

На основании принципа математической индукции заключаем, что исходное равенство истинно для любого nÎN.