Случайная величина и ее основные характеристики

Определение. Случайной величиной Х называется величина, принимающая то или иное заранее неизвестное числовое значение в зависимости от исхода испытания.

Определение. Дискретной случайной величиной называется величина, которая может принимать только конечное или счетное множество значений, т. е. такое множество, элементы которого можно пронумеровать.

Определение. Законом распределения дискретной случайной величины Х называется соответствие между возможными значениями Х и их вероятностями.

	x1	x2	…	xn
	p1	p2	…	рn

Причем, p₁ + p₂ +…+ p_n = 1.

Наиболее важными числовыми характеристиками случайной величины являются математическое ожидание М(Х), дисперсия D(X) и среднеквадратическое отклонение σ(Х).

Определение. Математическим ожиданием дискретной случайной величины Х называют сумму произведений всех ее возможных значений на соответствующие им вероятности:

.

Некоторые свойства математического ожидания:

1. M(C) = 0, где C=const;

2. M(CX) = C M(X);

3. M(X ± Y) = M(X) ± M(Y).

Замечание: называют средним значением случайной величины 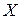. Физическая размерность совпадает с размерностью случайной величины .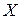

Определение. Дисперсией (рассеянием) дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Замечание: 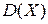характеризует степень рассеяния значений случайной величины 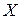около ее математического ожидания . Дисперсия 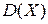имеет размерность квадрата случайной величины .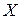

Некоторые свойства дисперсии:

1. D(C) = 0, где C=const;

2. D(CX) = C² D(X);

3. D(X) = M(X ²) – [M(X)]².

Среднеквадратическое отклонение дискретной случайной величины определяется по формуле: .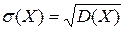

Пример:

Найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х, заданной таблицей:

	-1
	0,12	0,38	0,38	0,12

Решение.

;

Вычислим дисперсию по свойству:

;

.

.

Ответ: M(X)=0,5; D(X)=0,73; σ(Х)=0,844.