
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод минимизирующих карт Карно
При построении сокращенных ДНФ для функций, зависящих от небольшого числа (не более 4) переменных, используется метод карт Карно. Построение карт Карно основано на свойствах булева куба.
Множество всех двоичных наборов длины n образует n-мерный булев или двоичный куб, который называют также единичным n-мерным кубом и обычно обозначают  . Применяя геометрическую терминологию, наборы
. Применяя геометрическую терминологию, наборы  называют вершинами куба
называют вершинами куба  .
.
Расстоянием Хэмминга между вершинами  и
и 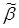 куба
куба  называется число
называется число  оно равно числу координат, в которых наборы
оно равно числу координат, в которых наборы  и
и 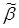 отличаются друг от друга. Расстояние Хемминга является метрикой, а куб
отличаются друг от друга. Расстояние Хемминга является метрикой, а куб  – метрическим пространством.
– метрическим пространством.
Наборы  и
и 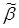 из
из  называются соседними если
называются соседними если  и противоположными если,
и противоположными если,  т.е. соседние наборы различаются только в одной координате, а противоположные во всех координатах.
т.е. соседние наборы различаются только в одной координате, а противоположные во всех координатах.
Символом  обозначают множество
обозначают множество  т.е. множество всех наборов
т.е. множество всех наборов  из
из  , на которых функция
, на которых функция  обращается в 1.
обращается в 1.
Гранью единичного n-мерного куба  называется множество
называется множество 
 Множество
Множество  называется направлением, число k - рангом, а число n–k – размерностью грани
называется направлением, число k - рангом, а число n–k – размерностью грани  . Кодом грани G=
. Кодом грани G=  называется вектор
называется вектор  длины n, в котором
длины n, в котором  , а остальные координаты есть «–». Например
, а остальные координаты есть «–». Например  =
=
(0–1–). Одномерные грани называются ребрами куба.
Обозначим множество векторов длины n с координатами из множества {0, 1, –} через Gn. На множестве Gn зададим частичный порядок, полагая 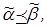 если вектор
если вектор 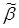 может быть получен из
может быть получен из  путем замены некоторых (быть может, ни одной) координат набора
путем замены некоторых (быть может, ни одной) координат набора  , равных 0 и 1, на «–». Отношение
, равных 0 и 1, на «–». Отношение  между кодами граней G и H соответствует отношению
между кодами граней G и H соответствует отношению  между гранями. Положим
между гранями. Положим  равным числу прочерков в наборе
равным числу прочерков в наборе  и
и  Тогда
Тогда 
 соответствует множеству ребер куба
соответствует множеству ребер куба  ,
,  – множеству граней куба
– множеству граней куба  , имеющих размерность k. Интервалом
, имеющих размерность k. Интервалом  куба
куба  называется множество вида
называется множество вида  , где
, где  ,
, 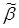 – вершины из
– вершины из  такие, что
такие, что  . Число
. Число  называется размерностью интервала.
называется размерностью интервала.
Если элементарная конъюнкция k является импликантой функции  , то множество Nk всех наборов
, то множество Nk всех наборов  и
и 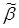 из
из  таких, что
таких, что  образует грань, содержащуюся в множестве Nf. Эта грань называется интервалом функции f, соответствующем импликанте k. Интервал функции f, не содержащийся ни в каком другом интервале функции f, называется максимальным интервалом. Максимальные интервалы функции f соответствуют ее простым импликантам.
образует грань, содержащуюся в множестве Nf. Эта грань называется интервалом функции f, соответствующем импликанте k. Интервал функции f, не содержащийся ни в каком другом интервале функции f, называется максимальным интервалом. Максимальные интервалы функции f соответствуют ее простым импликантам.
В методе минимизирующих карт Карно функция задается прямоугольной таблицей, в которой наборы значений переменных на каждой из сторон прямоугольника расположены в коде Грея. Нахождение простых импликант сводится к выделению максимальных по включению прямоугольников, состоящих из единиц. Из прямоугольников, соответствующих граням максимальной размерности, находим коды максимальных интервалов. Считается, что каждая клетка таблицы является соседней к клетке, примыкающей к противоположной стороне и расположенной на той же горизонтали или вертикали. Метод применим также и для не всюду определенных функций. В этом случае выделяются максимальные прямоугольники, содержащие хотя бы одну единицу и не содержащие нулей.
Пример 2. Таблица 3.12 представляет собой минимизирующую карту для функции  с вектором значений
с вектором значений  Коды максимальных интервалов имеют вид (00-0), (000-), (--01), (-1-1), (110-). Сокращенная ДНФ имеет вид
Коды максимальных интервалов имеют вид (00-0), (000-), (--01), (-1-1), (110-). Сокращенная ДНФ имеет вид 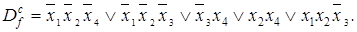
Таблица 3.12 Таблица 3.13


Пример 3. Таблица 3.13 представляет собой минимизирующую карту для частичной функции f, зависящей от трех переменных. Сокращенная ДНФ имеет вид 
Дата добавления: 2014-11-13; просмотров: 476; Мы поможем в написании вашей работы!; Нарушение авторских прав |