Алгоритм построения сокращенной ДНФ с помощью КНФ

(метод Нельсона)

Пусть f(x₁, … , x_n) есть некоторая функция алгебры логики. Построим для f некоторую КНФ. Осуществим далее следующие преобразования.

1. В КНФ раскроем скобки и удалим дублирующие члены, затем удалим дизъюнктивные слагаемые, содержащие одновременно переменную и ее отрицание. В результате получим дизъюнкцию конъюнкций, каждая из которых содержит только по одному элементу из каждой скобки КНФ.

2. В полученном выражении удалим нулевые дизъюнктивные слагаемые.

3. В полученном выражении проведем все поглощения, а затем удалим дублирующие члены.

В результате проведенных операций получим сокращенную ДНФ функции f. Покажем это.

Для каждой элементарной дизъюнкции D в КНФ и каждой элементарной конъюнкции K в сокращенной ДНФ (сокр. ДНФ) существует некоторый множитель вида x из K, содержащийся в D, т.е.

" DÎ ДНФ " K Î сокр. ДНФ $ x^a Î K (x^aÎ D).

Допустим противное: в КНФ существует элементарная конъюнкция D, в сокращенной ДНФ существует элементарная конъюнкция K, для которой всякий множитель вида x^a из K не входит в D. Не уменьшая общности возьмем для простоты

Положим x₁ = a₁, …, x_k=a_k, x_k+1 = c_k+1 ¹ a_k+1, …, x_r = c_r ¹ a_r. Тогда K(a₁, …, a_k) = 1, и потому f (a₁, …, a_k, c_k+1, …, c_r ) = 1. С другой стороны, D(c_k+1,…, c_r) = 0, и потому f (a₁, …, a_k, c_k+1, …, c_r ) = 0. Противоречие.

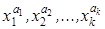Пусть по-прежнему для простоты произвольный простой импликант K из сокращенной ДНФ равен . Тогда элементы попадут в не менее чем k скобок из КНФ. Если допустим, что этого нет, то при перемножении скобок из КНФ не получим дизъюнктивного слагаемого, которое содержало бы множители 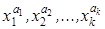, а потому, строя из результата перемножения сокращенную ДНФ вычеркиванием лишних сомножителей, не получим простого импликанта K.

Так как 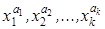содержатся в k разных скобках КНФ, а всякая другая скобка, отличная от указанных k скобок, содержит хотя бы один элемент вида x из K, то при раскрытии скобок имеем простой импликант K. После проведения всех операций поглощения и удаления дублирующих множителей, останутся только простые импликанты из сокращенной ДНФ, ибо если предположить наличие в результате хотя бы одного дизъюнктивного слагаемого, отличного от всех простых импликантов сокращенной ДНФ, то можно подобрать такие значения переменных функции f, на которых все простые импликанты примут значение 0, а это дополнительное слагаемое – значение 1, чего быть не может.

Пример 3. Построим сокращенную ДНФ этим способом для функции

f = (1111010010101111) из примера 1 :

Сокращенная ДНФ для функции

что, естественно, совпадает с результатом примера 1.

Пример 4. Построить сокращенную ДНФ по заданной КНФ

После раскрытия скобок имеем:

После второго этапа получаем сокращенную ДНФ:

Тупиковой ДНФ ( ТДНФ) функции f называется такая ДНФ ее простых импликант, из которых нельзя выбросить ни одного импликанта, не изменив функции f.

Теорема.Всякая минимальная ДНФ некоторой функции является ее тупиковой ДНФ.

Доказательство.В МДНФ входят только простые импликанты, иначе некоторые множители в непростом имликанте можно удалить в противоречие с минимальностью исходной ДНФ. В МДНФ нет лишних импликант, иначе исходная ДНФ не является минимальной.

Вывод.Для получения МДНФ функции f необходимо построить все ТДНФ функции f и выбрать из них те, которые содержат минимальное число букв.