
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение всех тупиковых ДНФ.
Пусть f(x1, …, xn) есть функция алгебры логики.
1. Построим СДНФ функции f, и пусть P1, P2, …,Pn есть ее коституенты единицы).
2. Построим сокращенную ДНФ функции, f и пусть K1, K2, …, Km – ее простые импликанты.
3. Построим матрицу покрытий простых импликант функции f ее конституентами единицы (табл. 3.4), полагая, что
+, если каждый множитель в Ki является множителем в Pj; (Pj есть aij= часть для Ki );
Æ в противном случае.
Таблица 3.4
| N | P1 P2 … Pj …Pn |
| K1 K2 Ki Km | a11 a12 … a1j …a1n a21 a22 … a2j … a2n ai1 ai2 … aij … ain am1 am2… amj … amn |
4. Для каждого столбца j ( 1 £ j £ n ) найдем множество Ej всех тех номеров I строк, для которых aij = 1. Пусть  Составим выражение
Составим выражение 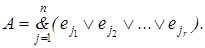 Назовем его решеточным выражением. Это выражение можно рассматривать как формулу, построенную в свободной дистрибутивной решетке с образующими 1, 2, …,m и с операциями & и Ú .
Назовем его решеточным выражением. Это выражение можно рассматривать как формулу, построенную в свободной дистрибутивной решетке с образующими 1, 2, …,m и с операциями & и Ú .
5. В выражении A раскроем скобки , приведя выражение A к равносильному выражению 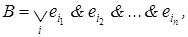 где перечислены все конъюнкции
где перечислены все конъюнкции  элементы
элементы 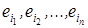 которой взяты из скобок 1,2,…,n соответственно в выражении A.
которой взяты из скобок 1,2,…,n соответственно в выражении A.
6. В выражении B проведем все операции удаления дублирующих членов и все операции поглощения. В результате получим дизъюнкцию элементарных конъюнкций C.
Утверждение.Каждая элементарная конъюнкция i1&i2&…&ir в С дает ТДНФ 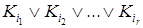 для f . Все ТДНФ для функции f исчерпываются элементарными конъюнкциями в выражении С.
для f . Все ТДНФ для функции f исчерпываются элементарными конъюнкциями в выражении С.
Пример 5. Сокращенная ДНФ для функции f = (1111010010101111) имеет вид 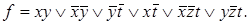
Для функции f построим все минимальные ДНФ.
1. Строим матрицу покрытий (таблица 3.5).
Таблица 3.5
| Конституенты единицы функции f | ||
| N | ПИ | x `x `x `x `x x x x x x x y `y `y `y y `y `y y y y y z `z z z `z `z z `z `z z z t t `t t t `t `t `t t t t |
| x y `x`y `y`t x`t `x`z t y`z t | + + + + + + + + + + + + + + + + + + + + |
2. Строим решеточное выражение (по столбцам таблицы).
E = (2Ú3)(2Ú5)(2Ú3)2(5Ú6)(3Ú4)(3Ú4)(1Ú4)(1Ú6)(1Ú4)(1) = (2Ú3)(2Ú5)(5Ú6)(3Ú4)(1Ú4)(1Ú6)12 = (5Ú6)(3Ú4)(1)(2) = 1235Ú1245Ú1236Ú1246.
3. Строим все тупиковые ДНФ функции f:
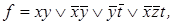 простые импликанты 1,2,3,5;
простые импликанты 1,2,3,5;
 простые импликанты 1,2,4,5;
простые импликанты 1,2,4,5;
 простые импликанты 1,2,3,6;
простые импликанты 1,2,3,6;
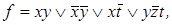 простые импликанты 1,2,4,6.
простые импликанты 1,2,4,6.
4. Все найденные ТДНФ являются минимальными ДНФ.
Дата добавления: 2014-11-13; просмотров: 371; Мы поможем в написании вашей работы!; Нарушение авторских прав |