Задачи по минимизации и доопределению булевых функций

1. Из заданного множества А элементарных конъюнкций выделить простые импликанты функции f :

1) A = , = (00101111);

2) A = , = (01111110);

3) A = , = (1010111001011110);

4) A = , = (1011);

5) A = , = (00111011);

6) A = 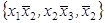, = (00101111).

2.По заданной ДНФ с помощью метода Блейка построить сокращенную ДНФ:

1)

2)

3)

4)

5)

6)

7)

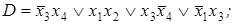
8)

3. Построить сокращенную ДНФ по заданной КНФ:

1)

2)

3)

4)

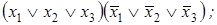
5)

6)

7)

8)

4.Изобразив множество N_f функции в E_n, найдйте коды максимальных интервалов и построитьйте сокращенную ДНФ:

1) = (11110100); 2) = (01010011);

3) = (11010011); 4) = (11100111);

5) = (1111100001001100); 6) = (0001011111101111);

7) = (1110011000000111); 8) = (1111111111111000).

5. С помощью алгоритма Квайна построить сокращенную ДНФ для функции f, заданной вектором своих значений:

1) = (01110110); 2) = (10111101);

3) = (00101111); 4) = (11100100);

5) = (0001101111011011); 6) = (0000111111110110);

7) = (1111111101111110); 8) = (0000111101111111).

6. Найти сокращенную ДНФ функции f с помощью минимизирующей карты:

1) = (01010111); 2) = (11011011);

3) = (10110000); 4) = (11101111);

5) = (0001101111011111); 6) = (0011110111111101);

7) = (0011110111011110); 8) = (0010101111011111).

7. С помощью минимизирующих карт построить сокращенную ДНФ для частично определенной функции f, заданной векторно (прочерки соответсвуют неопределенным значениям):

1) = (01--01-1);

2) = (1-01--10);

3) = (1---0-10);

4) = (0--10-1-);

5) = (10-1-011-0--1-01);

6) = (0--1---0--1-1-01);

7) = (--01-1-00----1-0);

8) = (-10-1-11-01-0---).

8. Найти длину сокращенной ДНФ функции f:

1)

2)

3)

4)

5)

6)

7)

8)

9)

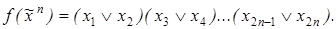
9. Выяснить, является ли ДНФ D а) тупиковой, б) кратчайшей, в)минимальной:

1)

2)

3)

4)

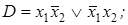
5)

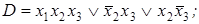
6)

7)

8)

10. Применить алгоритм упрощения к ДНФ:

1)

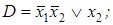
2)

3)

4)

5)

6)

7)

8)

11. По заданной сокращенной ДНФ D построить минимальные ДНФ:

1)

2)

3)

4)

5)

6)

7)

8)

12. С помощью таблицы Квайна построить все тупиковые ДНФ функции f, заданной вектором своих значений:

1) = (01111100); 2) = (01111110);

3) = (00011111); 4) = (1111100001001100);

5) = (1110100001101000); 6) = (1110011000010101);

7) = (0001011110101110); 8) = (0001101111100111).