Критерий Найквиста

Устойчивость замкнутой системы определяется по годографу комплексной частотной характеристики разомкнутой системы.

Обратимся к передаточной функции разомкнутой системы,

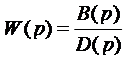. (2.6)

Характеристический полином есть D(p) . Устойчивость разомкнутой системы определяется по характеристическому полиному D(p) .

Иными словами он содержит в себе информацию об устойчивости разомкнутой системы. Если система замкнутая, ее передаточная функция

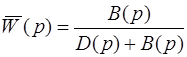. (5.4)

Характеристический полином есть D(p) + B(p) . Устойчивость замкнутой системы определяется по характеристическому полиному D(p) + B(p) . То есть, в нем содержится информация об устойчивости замкнутой системы. Отношение передаточных функций (2.6) и (5.4) есть отношение характеристического полинома замкнутой системы к характеристическому полиному разомкнутой системы:

.

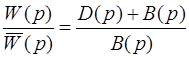Значит, содержит в себе информацию об устойчивости как замкнутой, так и разомкнутой системы. Устойчивость замкнутой системы связана с устойчивостью разомкнутой. Поскольку 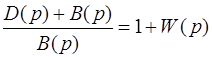, (5.10)

открываются возможности судить об устойчивости замкнутой системы по передаточной функции разомкнутой системы. Запишем выражение (5.10) в частотной форме, полагая p = jw : 1 + W(jw) .

W(jw) есть комплексная частотная характеристика разомкнутой системы. Эту характеристику можно изобразить графически на комплексной плоскости, задавая w от 0 до ∞ и рассчитывая частотные характеристики: действительную U(w) и мнимую V(w) . Получается годограф разомкнутой системы. Его вид говорит об устойчивости или неустойчивости замкнутой системы.

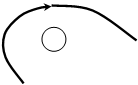
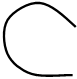
Допустим, разомкнутая система устойчива. Тогда, если годограф устойчивой разомкнутой системы при изменении w от 0 до ∞ не охватывает точку -1 на оси абсцисс, то замкнутая система будет устойчивой. Охватывает – замкнутая система неустойчивая.

Примеры годографов, соответствующих устойчивой и неустойчивой замкнутой системам, представлены на рис. 5.14 и 5.15 .

V V

-1 -1

Рис. 5.14 Рис. 5.15

V V

-1 -1

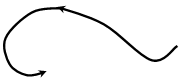
Рис. 5.16 Рис. 5.17

V V

-1 -1

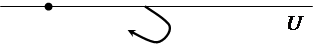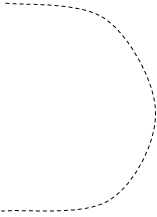
Рис. 5.18 Рис. 5.19

Замкнутая система может быть устойчивой и тогда, когда разомкнутая система неустойчива.

Критерий Найквиста для неустойчивой разомкнутой системы: если годограф неустойчивой разомкнутой системы при изменении w от 0 до ∞ охватывает точку -1 на оси абсцисс в положительном направлении m / 2 раз, где m – число корней характеристического уравнения разомкнутой системы с положительной действительной частью, то замкнутая система будет устойчивой. (положительной считается движение конца вектора против часовой стрелки).

Примеры годографов, соответствующих устойчивой и неустойчивой замкнутым системам во втором случае, представлены на рис. 5.16 и 5.17 для m = 2 .

Если разомкнутая система имеет передаточную функцию, содержащую в знаменателе множителем комплексную переменную р , ,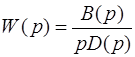

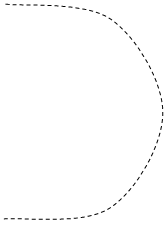
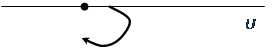
то комплексная частотная характеристика будет иметь неопределенность при w = 0 . Амплитуда становиться бесконечной. Годограф получается с бесконечной ветвью. Но если годограф мысленно дополнить зеркально отраженной ветвью и провести полуокружность бесконечно большого радиуса так, чтобы она пересекала положительную часть оси абсцисс, то такой прием позволяет использовать первую формулировку критерия Найквиста. То есть, если точка -1 на оси абсцисс лежит за пределами замкнутой кривой – замкнутая система устойчивая. Если охватывается кривой – неустойчивая. Примеры таких годографов приведены на рис. 5.18 и 5.19 .

Подведем итог сказанному в виде таблицы 1, с использованием соответствующих аббревиатур.

Таблица 1

РСУ . Тогда ЗСУ, если -1 вне.

ЗСН, если -1 внутри.

РСН . Тогда ЗСУ, если -1 вне.

ЗСН, если -1 внутри.

РС

астатическая. Тогда ЗСУ, если -1 вне.

ЗСН, если -1 внутри.

Замкнутая система будет находиться на границе устойчивости, если годограф разомкнутой системы проходит через точку -1 оси абсцисс. Аналитически это условие можно записать в виде 1 + W(jw) = 0 .

Кривые Найквиста наглядно показывают влияние коэффициента усиления на устойчивость системы. Для передаточной функции, в которой коэффициент усиления увеличивают, размеры и положение кривой Найквиста меняются относительно точки с координатой (-1,0). Допустим, имеется кривая 1, отвечающая границе устойчивости, рис.5.20. Предельный коэффициент усиления k = k^*. Кривая 2, для которой k < k^*, отвечает устойчивой системе, кривая 3, для которой

k > k^* - неустойчивой. Увеличение коэффициента усиления вызывает смещение влево точки пересечения кривой 2 с отрицательной частью действительной оси. То есть, может перевести систему из устойчивого состояния в неустойчивое.

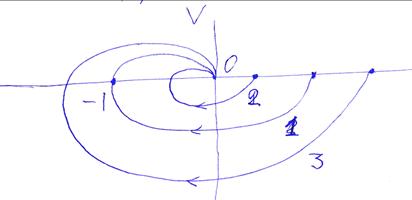
Рис. 5.20. Значение коэффициентов усиления:

1 - k = k^*, 2 - k< k^*, 3 – k > k^*.

Система, имеющая годограф, изображенный на рис. 5.20, с увеличением коэффициента усиления способна реализовать два состояния: «устойчивость – неустойчивость». Для более сложных кривых число состояний может увеличиваться. Например, у кривой с одним максимумом в отрицательной полуплоскости (рис. 5.21) по мере

Рис. 5.21 Рис. 5.22

увеличения коэффициента усиления устойчивое состояние сменяется неустойчивым, а затем снова устойчивым. У кривой с двумя максимумами (рис.5.22), при увеличении коэффициента усиления, реализуются состояния: «устойчивость – неустойчивость – устойчивость – неустойчивость». Система может устойчиво работать в двух разных интервалах изменения коэффициента усиления. Это свойство не обнаруживается применением критерия Гурвица или Михайлова.

Коэффициент усиления на границе устойчивости рассчитывают, приравнивая комплексную частотную характеристику минус единице:

W(jw) = -1.

40. Выделение области устойчивости методом D – разбиения

Устойчивость системы автоматического регулирования зависит от того, какими будут коэффициенты дифференциального уравнения, которое её описывает. Одна часть коэффициентов обеспечивает устойчивые решения дифференциального уравнения, другая часть – дополняющая первую - обеспечивает неустойчивые решения.

Идея метода D - разбиения заключается в том, чтобы найти границу между этими коэффициентами и тем самым указать область устойчивости. Для этого выделяют один или два важных коэффициента, изменяют их и исследуют, как меняются корни характеристического уравнения. Все остальные коэффициенты фиксируются.

Пусть дано характеристическое уравнение системы автоматического регулирования: 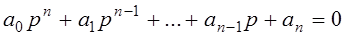. (2.7.)

Пусть все коэффициенты заданы, кроме a₀ и a_n. Предположим, что уравнение (2.7.) имеет в плоскости корней kкорней слева от мнимой оси и n - kкорней справа для каких–то значений a₀ и a_n , рис. 5.21.

V p a₀

k n-k

D(k, n-k)

0 a_n

Рис. 5.21 Рис 5.22

Будем менять значения коэффициентов a₀ и a_n и находить корни. Возможно, для некоторой совокупности значений a₀ и a_n количество корней слева и справа от мнимой оси не меняется. Т. е. соотношение между k и n-k остается постоянным. Тогда как совокупность других значений коэффициентов a₀ и a_n меняет соотношение между kи n–k. Можно указать границу, отделяющую область постоянного отношения kи n-k. Эту область обозначают D(k, n - k), рис. 5.22.

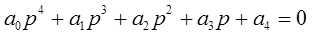Например, для характеристического уравнения четвертой степени

в плоскости коэффициентов могут быть следующие области:

D(0,4), D(1,3), D(2,2), D(3,1), D(4,0).

Всего n + 1 областей.

Из всех D(k, n - k) областью устойчивости будет только одна: D(n, 0). В ней все корни, располагающиеся слева от мнимой оси, имеют отрицательную действительную часть. Мнимая ось – граница устойчивости в плоскости корней. В плоскости коэффициентов кривая, отделяющая область устойчивости от области неустойчивости, будет ничем иным, как преобразованной мнимой осью.

41. D – разбиение по одному параметру

Изучение метода D - разбиения начнем с выяснения влияния на устойчивость одного параметра. При заданных значениях других параметров. Обозначим параметр символом 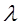. Это может быть коэффициент характеристического уравнения, или сочетание коэффициентов. Например, в уравнении

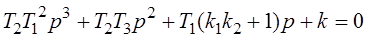
Можно назвать параметром T₁, T₂, T₃, k.

Допустим, сделан выбор l = T₂. Тогда уравнение примет вид

l(T₁²p³ + T₃p²) + T₁(k+1)p+k = 0 .

Полином, который умножается на l , обозначим Q(p), остальную часть S(p). Уравнение примет общий вид:l Q(p) + S(p)=0 . (5.4)

Представив уравнение (5.4) в виде 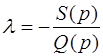, (5.5)

получаем 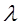как функцию переменной p.

Чтобы построить границы области устойчивости, полагаем

p = jw. Тогда l(p) становится комплексным числом: l(jω) = - 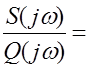U(ω)+jV(ω

Если теперь задавать ω от 0 до +¥, вектор l(jω) вычертит некоторую кривую на комплексной плоскости U, V. Эта кривая отображает на плоскость U, V мнимую ось комплексной плоскости корней, то есть будет границей, по одну сторону которой k корней, по другую n - k.

Если задавать ω от 0 до -¥, получится зеркальное отображение кривой для +ω. Поэтому кривую рассчитывают для положительных ω, а затем дополняют зеркальным отображением относительно действительной оси.

Чтобы разобраться, по какую сторону находятся kкорней, область D - разбиения выделяется штриховкой. Соображения следующие.

При движении по мнимой оси в плоскости корней (рис. 5.23) от 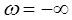до 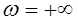та область, в которой находятся все корни устойчивости будет все время слева. Она показана штриховкой.

V

Корни

устойчивости

w ® -¥

Рис. 5.23. Рис. 5.24

Требуется, чтобы и в плоскости 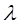область устойчивости находилась слева от кривой D-разбиения, если двигаться от 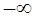к . Левая сторона кривой штрихуется.

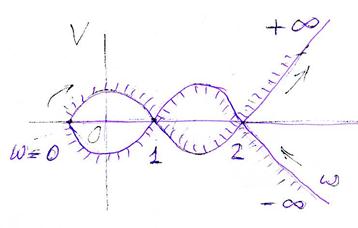
Рассмотрим в качестве примера кривую, изображенную на рисунке 5.24. На этой кривой показано, как надо наносить штриховку. Область устойчивости ограничена кривой со штриховкой внутрь.

Параметр 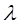по физическому смыслу есть величина действительная, поэтому для расчетов используется только отрезок действительной оси, охваченной кривыми со штриховкой внутрь:

от точки 1 до точки 2. (рис. 5.24) .