Уравнение гармонических колебаний

,

где x – смещение точки от положения равновесия; A – амплитуда колебаний ( = x_max); – циклическая частота колебаний; t– время; – начальная фаза колебаний; – фаза колебаний в момент времени t.

2. Циклическая частота

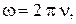
где T – период колебаний; – частота колебаний.

3. Скорость и ускорение колеблющейся материальной точки

.

4. Сила, под действием которой материальная точка массой m совершает колебания

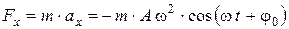
или

где – коэффициент упругости; F_x – квазиупругая сила.

5. Полная энергия материальной точки, совершающей гармонические колебания

6. Период колебаний гармонического осциллятора:

1) физического маятника

где I – момент инерции колеблющегося тела относительно оси колебаний; b – расстояние от центра масс тела до оси колебаний; g – ускорение свободного падения; 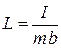– приведённая длина физического маятника;

2) математического маятника

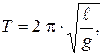
где – длина маятника;

3) пружинного маятника ( тела, подвешенного на пружине; масса пружины мала по сравнению с массой тела)

где m – масса тела; k – жесткость пружины;

4) идеального колебательного контура

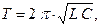
где L – индуктивность контура; С – электроёмкость контура.

7. Координаты центра масс системы материальных точек

где 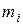– масса 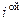материальной точки; – её координаты.

8. При сложении двух одинаково направленных гармонических колебаний одинаковой частоты получается гармоническое колебание того же периода с амплитудой

и начальной фазой

где 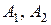– амплитуды складываемых колебаний; 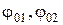– их начальные фазы ( , то есть разность фаз в любой момент времени равна разности начальных фаз).

9. При сложении двух взаимно перпендикулярных колебаний одинаковой частоты уравнение траектории результирующего движения в координатах x, y имеет вид

а) если

б) если

в) 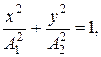если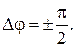

10. Дифференциальное уравнение свободных, незатухающих гармонических колебаний материальной точки

где – вторая производная смещения по времени (физический смысл – ускорение).

Решение этого уравнения

где – собственная циклическая частота ( ).

11. Дифференциальное уравнение затухающих колебаний

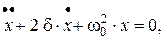
где – коэффициент затухания ( ); r – коэффициент сопротивления
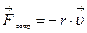( ); – собственная циклическая частота ( ).

Решение этого уравнения

где – амплитуда затухающих колебаний; – амплитуда колебаний в момент времени – циклическая частота затухающих колебаний ( ).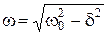

12. Логарифмический декремент затухания

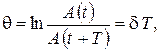
где 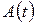и – амплитуды двух последующих колебаний, отстоящих по времени друг от друга на период.

13. Дифференциальное уравнение вынужденных колебаний

где ; 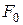– амплитудное значение вынуждающей силы ; – частота изменения вынуждающей силы.

Решение этого уравнения

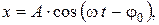
где А – амплитуда вынужденных колебаний; – частота изменения вынуждающей силы.

;

– начальная фаза вынужденных колебаний

.

14. Резонансная частота и резонансная амплитуда