
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры элементарных преобразований
Продемонстрируем все элементарные преобразования на примере матрицы 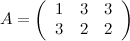
Умножим первую строку матрицы на два, то есть каждый элемент первой строки умножаем на двойку, в результате получим матрицу 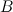 , эквивалентную заданной матрице
, эквивалентную заданной матрице 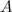 :
:
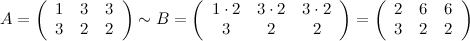
Поменяем первую и вторую строки матрицы 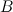 местами, получаем эквивалентную ей матрицу
местами, получаем эквивалентную ей матрицу 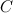 :
:
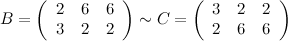
От первой строки матрицы 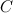 отнимем вторую строку, получаем эквивалентную матрицу
отнимем вторую строку, получаем эквивалентную матрицу 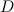 :
:
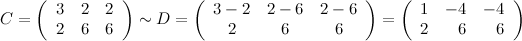
В итоге делаем вывод, что матрицы 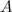 и
и 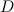 эквивалентны, так как от одной из них перешли к другой при помощи эквивалентных преобразований над строками.
эквивалентны, так как от одной из них перешли к другой при помощи эквивалентных преобразований над строками.
Линейно зависимые, линейно независимые строки матрицы. Критерий линейной зависимости.
Линейной комбинацией (ЛК) строк 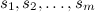 матрицы
матрицы 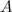 называется выражение
называется выражение 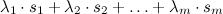
ЛК называется тривиальной, если все коэффициенты 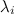 равны нулю одновременно.
равны нулю одновременно.
Пример
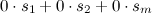
Замечание:Тривиальная ЛК равна нулевой строке.
ЛК называется нетривиальной, если хотя бы один из коэффициентов 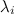 отличен от нуля.
отличен от нуля.
Пример
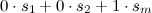
Замечание:Нетривиальная ЛК тоже может быть равной нулевой строке.
Пример
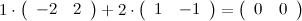
Дата добавления: 2015-04-11; просмотров: 202; Мы поможем в написании вашей работы!; Нарушение авторских прав |