Системы линейных алгебраических уравнений (СЛАУ).

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

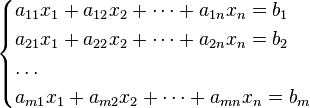
(1)

Система линейных уравнений от трёх переменных определяет набор плоскостей. Точка пересечения является решением.

Здесь 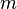— количество уравнений, а — количество неизвестных. x₁, x₂, …,x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[2].

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

Упорядоченный набор значений 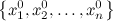называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.