
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определители матриц, их свойства.
Понятие определителя матрицы
Квадратной матрице  n –го порядка ставиться в
n –го порядка ставиться в
соответствие число  , называемое определителем матрицы или детерминантом.
, называемое определителем матрицы или детерминантом.
Свойства определителей:
Замечание
Все что будет сказано относительно строк, будет относиться и к столбцам.
1° При транспонировании квадратной матрицы её определитель не меняется: 
2° Общий множитель в строке можно выносить за знак определителя.
3°  То есть, если квадратная матрица
То есть, если квадратная матрица 
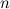 -го порядка умножается на некоторое ненулевое число
-го порядка умножается на некоторое ненулевое число  , то определитель полученной матрицы равен произведению определителя исходной матрицы
, то определитель полученной матрицы равен произведению определителя исходной матрицы 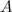 на число
на число  в степени, равной порядку матриц.
в степени, равной порядку матриц.
4° Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

5° Если две строки определителя поменять местами, то определитель поменяет знак.
6° Определитель с двумя равными строками равен нулю.
7° Определитель с двумя пропорциональными строками равен нулю.
8° Определитель, содержащий нулевую строку, равен нулю.
9° Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
10° Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
11° Определитель произведения матриц равен произведению определителей: 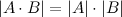
Дата добавления: 2015-04-11; просмотров: 209; Мы поможем в написании вашей работы!; Нарушение авторских прав |