Критерий совместности СЛАУ Кронекера-Капелли.

Теорема Кронекера-Капелли. СЛАУ совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Задание. При каких значениях система будет совместной?

Решение. Ранг матрицы равен количеству ненулевых строк после приведения этой матрицы к ступенчатому виду. Поэтому записываемрасширенную матрицу системы (слева от вертикальной черты находится матрица системы ):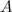

и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от первой строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:

Третью строку складываем с первой:

и меняем первую и вторую строки матрицы местами

Матрица приведена к ступенчатому виду. Получаем, что 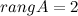, . Таким образом, при система совместна, а при - несовместна.