Векторный способ описания движения

Положение движущейся материальной точки определяется уравнением:

, (1.1)

где радиус вектор движущейся точки (см. рис.1.1).

Вектор перемещения соединяет начальное и конечное положение движущейся точки, и направлен от начального положения к конечному положению:

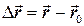. (1.2)

Для характеристики быстроты движения вводится понятие средней и мгновенной скорости. Средняя скорость – отношение перемещения точки ко времени:

. (1.3)

Так как , то вектор средней скорости всегда направлен по перемещению,т.е. .Можно также ввести понятие средней путевой скорости движения. Средней путевой скоростью движения точки называется отношение пройденного пути к интервалу времени движения точки. Так как пройденный путь величина скалярная, то и средняя путевая скорость является скалярной величиной.

Предельное значение, к которому стремится вектор средней скорости при стремлении интервала времени к нулю, называется мгновенной скоростью. Обозначение мгновенной скорости:

(1.4)

Такие пределы в математике получили название производной, т.е. мгновенная скорость - это производная от перемещения по времени. Мгновенная скорость характеризует скорость тела в данной точке в данный момент времени. Мгновенная скорость всегда направлена по касательной к траектории движения.

Для характеристики быстроты изменения скорости вводят понятие ускорения движения. Средним ускорением называется отношение вектора изменения скорости к интервалу времени, в течение которого это изменение произошло, т.е.:

(1.5)

Так как , то вектор среднего ускорения всегда направлен по вектору изменения мгновенной скорости, т.е. (см. рис. 1.2). Предельное значение, к которому стремится вектор среднего ускорения при условии, что интервал времени стремится к нулю, называется мгновенным ускорением.

Мгновенное ускорение — это производная от вектора скорости по времени. Мгновенное ускорение показывает, как быстро изменяется вектор скорости движущейся точки. Обозначение мгновенного ускорения:

(1.6)