Вращение тела вокруг неподвижной оси

При вращении твердого тела вокруг закрепленной оси, траектории движения всех точек тела представляют собой окружности с центрами, лежащими на оси вращения. Это позволяет описать движение какой либо одной точки тела, поскольку движение остальных точек является подобным. 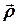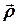Для описания вращательного движения точки используют полярную систему координат, в которой положение точки задается координатами: углом между радиус–вектором , проведенным из начала отсчета (точка ) и полярной осью и радиус–вектором (см. рис. 1.4). Начало отсчета совмещают с центром вращения точки, при таком выборе точки будет меняться только угол поворота. Используют при этом псевдо вектор угла , который по величине равен углу , измеренному в радианах. Направление вектора определяется по правилу буравчика. Вращаем буравчик от полярной оси в направлении радиус–вектора 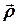, при этом поступательное движение буравчика указывает на направление вектора .

Пусть за бесконечно малый промежуток времени , твердое тело повернулось вокруг оси на угол (см. рис. 1.4). Вектор радиуса вращения обозначим , радиус–вектор точки –– , а перемещение некоторой точки твердого тела – .

Вектором угла поворота называется вектор, направленный по оси вращения, а его величина равна углу поворота , измеренному в радианах. Направление вектора определяют по правилу буравчика. Вращая буравчик по направлению вращения точки, при этом направление его поступательного движение укажет направление вектора угла поворота .

Из рисунка 1.4 видно, что величина бесконечно малого перемещения и угол поворота связаны соотношением

. (1.26)

Справедливо так е и векторное равенство:

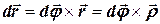. (1.27)

Для характеристики быстроты изменения угла поворота вводят понятие вектора угловой скорости. Угловая скорость есть производная от угла поворота по времени:

. (1.28)

Вектор угловой скорости направлен по оси вращения, его направление совпадает с направлением вектора бесконечно малого поворота .

Вектор углового ускорения характеризует быстроту изменения вектора угловой скорости, и находится как производная от вектора угловой скорости по времени:

. (1.29)

Направление вектора совпадает с направлением вектора бесконечно малого изменения угловой скорости . При ускоренном характере вращения тела направление вектора углового ускорения совпадает с направлением векторов бесконечно малого угла поворота и угловой скорости, при замедленном характере вращения вектор углового ускорения направлен против вектора угловой скорости.

Уравнением вращения тела вокруг неподвижной оси является зависимость вектора угла поворота от времени:

.

При решении задач используется проекция этого равенства на ось вращения (ось OZ). Ось OZ направляют по вектору угла поворота.

Примеры уравнений вращения тела вокруг неподвижной оси

1. Равномерное вращение тела ( ):

, (1.30)

где величина угла поворота в начальный момент времени, величина вектора угловой скорости.

2. Вращение с постоянным угловым ускорением ( ):

, (1.31)

где проекция вектора углового ускорения на ось OZ.

Зависимость угловой скорости от времени:

. (1.32)

Вопросы для самоконтроля.

1. Какая система координат используется для описания движения точки по окружности? Какими координатами задается положение вращающейся точки на плоскости?

2. Сформулируйте определение псевдовектора угла поворота. Как определяется величина и направление этого вектора?

3. Дайте определение вектора угловой скорости. Как определяется направление данного вектора?

4. Дайте определение вектора углового ускорения. Как связаны между собой направления векторов угловой скорости и углового ускорения при ускоренном и замедленном движениях?

5. Какова зависимость угла от времени при равномерном движении точки по окружности?

6. Какими соотношениями описывается движение точки с постоянным угловым ускорением по окружности?