
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Связь между линейными и угловыми величинами
Модуль вектора перемещения  и изменение угла поворота
и изменение угла поворота  связаны соотношением:
связаны соотношением:
 , (1.33)
, (1.33)
где 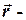 радиус–вектор точки
радиус–вектор точки  ,
,  ее радиус вращения (см. рис. 1.4).
ее радиус вращения (см. рис. 1.4).
Вектор линейной скорости 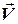 и вектор угловой скорости
и вектор угловой скорости  связаны векторным равенством:
связаны векторным равенством:
 . (1.34)
. (1.34)
В скалярном виде справедливо равенство:
 . (1.35)
. (1.35)
Для вектора полного ускорения  справедливы соотношения (1.20)–(1.23), и, кроме того, имеем следующее векторное равенство:
справедливы соотношения (1.20)–(1.23), и, кроме того, имеем следующее векторное равенство:
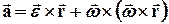 , (1.36)
, (1.36)
где 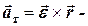 вектор тангенциального ускорения,
вектор тангенциального ускорения, 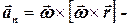 вектор нормального ускорения.
вектор нормального ускорения.
Проекции вектора  на орты
на орты  и
и 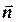 (см. рис. 1.3) равны:
(см. рис. 1.3) равны:
 ,
,  . (1.37)
. (1.37)
Модуль полного ускорения равен:
 . (1.38)
. (1.38)
Вопросы для самоконтроля.
1. Каким соотношением связаны между собой линейная и угловая скорость точки?
2. Каким соотношением связаны между собой угловое ускорение точки с ее тангенциальным ускорением?
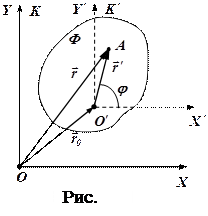
3. Каким соотношением связаны между собой угловая скорость точки с ее нормальным ускорением?
 §1.7. Плоское движение твердого тела
§1.7. Плоское движение твердого тела
Плоское движение – такое движение, при котором траектории всех точек тела лежат в параллельных плоскостях неподвижных в некоторой системе отсчета.
Примером плоского движения служит качение цилиндра по плоскости. Такое движение твердого тела можно представить как результат сложения двух движений, поступательного и вращательного.
Выберем две системы отсчета 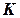 и
и  (см. рис. 1.5). Пусть система
(см. рис. 1.5). Пусть система  , связанная жестко с точкой
, связанная жестко с точкой 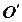 твердого тела движется поступательно относительно системы
твердого тела движется поступательно относительно системы 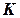 (см. рис 1.5).
(см. рис 1.5).
 При плоском движении тела его положение в процессе движения определяется положением такого сечения тела
При плоском движении тела его положение в процессе движения определяется положением такого сечения тела 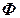 , которое лежит в плоскости траектории
, которое лежит в плоскости траектории 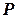 некоторой точки
некоторой точки  .
.
Положение сечения 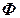 в системе отсчета
в системе отсчета 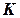 определяется радиус–вектором
определяется радиус–вектором 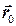 произвольной ее точки
произвольной ее точки 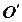 и углом
и углом 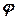 между осью
между осью  и вектором
и вектором 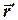 точки
точки  .
.
Заметим, что для абсолютно твердого тела модуль вектора 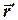 не зависит от времени (вектор
не зависит от времени (вектор 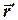 может только вращаться). Поэтому движение рассматриваемого сечения
может только вращаться). Поэтому движение рассматриваемого сечения 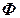 в системе
в системе 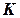 описывается уравнениями:
описывается уравнениями:
 . (1.39)
. (1.39)
Для точки  рассматриваемого сечения векторы
рассматриваемого сечения векторы 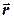 и
и 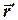 в системах отсчета
в системах отсчета 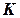 и
и  связаны соотношением:
связаны соотношением:
 , (1.40)
, (1.40)
Для бесконечно малых перемещений имеем равенство:
 , (1.41)
, (1.41)
где 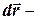 перемещение точки
перемещение точки  в системе
в системе 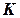 ,
, 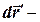 перемещение точки
перемещение точки  в системе
в системе  ,
, 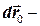 перемещение начала отсчета (точка
перемещение начала отсчета (точка 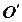 ) системы
) системы  относительно
относительно 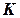 .
.
Скорость точки  в системе отсчета
в системе отсчета  и угловая скорость ее в системе
и угловая скорость ее в системе  связаны соотношением:
связаны соотношением:
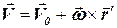 . (1.42)
. (1.42)
Из (1.42) видно, что скорость любой точки рассматриваемого сечения складывается из скорости поступательного движения 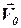 произвольной точки
произвольной точки  этого сечения и линейной скорости
этого сечения и линейной скорости 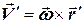 , обусловленной вращением вектора
, обусловленной вращением вектора  вокруг точки
вокруг точки  .
.
Очевидно, что векторы 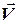 и
и 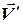 лежат в плоскости сечения
лежат в плоскости сечения 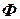 . Следовательно, можно найти такую точку
. Следовательно, можно найти такую точку 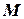 (не обязательно принадлежащую данному телу), линейная скорость которой в системе
(не обязательно принадлежащую данному телу), линейная скорость которой в системе  равна нулю. Это достигается тогда, когда
равна нулю. Это достигается тогда, когда  (см. рис. 1.6).
(см. рис. 1.6).
Ось, перпендикулярная сечению 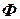 и проходящая через точку
и проходящая через точку 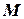 , называют мгновенной осью вращения. В этом случае плоское движение тела сводится к чисто вращательному движению вокруг мгновенной оси.
, называют мгновенной осью вращения. В этом случае плоское движение тела сводится к чисто вращательному движению вокруг мгновенной оси.
Дата добавления: 2015-04-15; просмотров: 392; Мы поможем в написании вашей работы!; Нарушение авторских прав |