Плоскость в R3.

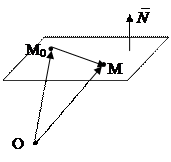Рассмотрим ПДСК {O,`i,`j,`k} в пространстве R<sup>3</sup>. Пусть a – некоторая плоскость и вектор `N перпендикулярен a. Зафиксируем на плоскости a произвольную точку М₀ и возьмем текущую точку М пространства.. Обозначим `r = и`r₀ = . Тогда 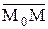= `r –`r₀, а точка МÎa тогда и только тогда, когда векторы `N и 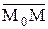ортогональны. Последнее возможно, когда

`N . 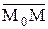= 0, т.е. `N .(`r –`r₀) = 0, (9)

это уравнение называется векторным уравнением плоскости. Вектор `N называют нормальным вектором плоскости.

Если `N =(А, В, С), М₀(х₀, у₀, z₀) , М(х, у, z) , то уравнение (9) примет вид

А(х – х₀) + В( у – у₀) + С(z – z₀) = 0, (10).

Это уравнение называют уравнением плоскости, проходящей через заданную точку перпендикулярно заданному вектору.

Как известно, через три точки можно провести единственную плоскость. Пусть М₁(х₁, у₁, z₁), М₃(х₂, у₂, z₂), М₃(х₃, у₃, z₃)Îa. Найдем уравнение этой плоскости. Согласно векторному уравнению (9), чтобы записать это уравнение, необходимо знать точку плоскости и нормальный вектор. Точка у нас есть (например М₁). А в качестве нормального вектора подойдет любой вектор, перпендикулярный этой плоскости. Известно, что векторное произведение двух векторов перпендикулярно плоскости, в которой лежат эти векторы. Следовательно, векторное произведение векторов 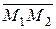и можно взять в качестве нормального вектора плоскости a:

`N = ´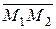

Тогда уравнение плоскости a в векторной форме имеет вид

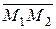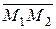.( ´ ) = . . = 0.

(заметим, что получили условие компланарности векторов , , ).

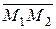Через координаты точек М₁, М₂, М₃ и М это уравнение запишется так

, (11)

и называется уравнением плоскости, проходящей через три заданные точки М₁(х₁, у₁, z₁), М₂(х₂, у₂, z₂), М₃(х₃, у₃, z₃).

Рассмотрим вновь уравнение (9), преобразуем его:

Ах + Ву + Cz +(–Ах₀ – Ву₀ – Cz₀) = 0 ,

Ах + Ву + Cz +D = 0, где D = (–Ах₀ – Ву₀ – Cz₀) .

Уравнение

Ах + Ву + Cz +D = 0, (12)

называетсяобщим уравнением плоскости. Здесь вектор`N = (A, B, C) – нормальный вектор плоскости (т.е. вектор, перпендикулярный плоскости).
Справедлива теорема:

Теорема 4.2.

В пространстве R³ всякая плоскость может быть описана линейным относительно переменных x y, z уравнением и наоборот, любое уравнение первой степени определяет некоторую плоскость.

Изучим расположение плоскости относительно системы координат по ее общему уравнению Ах + Ву + Cz +D = 0 .

Если коэффициент D = 0, то координаты точки О(0, 0, 0) удовлетворяют уравнению Ах + Ву + Cz = 0, значит, эта точка лежит на плоскости, т.е. плоскость с уравнением Ах + Ву + Cz = 0 проходит через начало координат.

Если в общем уравнении плоскости отсутствует одна из переменных (соответствующий коэффициент равен нулю), то плоскость параллельна одноименной оси координат. Например, уравнение Ах + Cz + D = 0 определяет плоскость, параллельную оси ОУ. Действительно, вектор нормали имеет координаты `N = (А, 0, С) и легко проверить, что `N^`j. Но если плоскость и вектор перпендикулярны одному и тому же вектору, то они параллельны. Плоскость с уравнением Ву + Cz = 0, в таком случае, проходит через ось ОХ (т.е. эта ось лежит на плоскости)

Отсутствие двух переменных в уравнении плоскости означает, что плоскость параллельна соответствующей координатной плоскости, например, уравнение вида Ах + D = 0 определяет плоскость, параллельную плоскости УОZ. Вектор нормали имеет координаты `N = (А, 0, 0), он коллинеарен вектору `i, и ,следовательно, плоскость перпендикулярна вектору `i , или параллельна плоскости УОZ.

Уравнения координатных плоскостей имеют вид:

пл. ХОУ: z = 0, пл. XOZ: y = 0, пл. YOZ: x = 0.

Действительно, плоскость ХОУ проходит через начало координат (D = 0) и вектор `k =(0, 0, 1) – ее нормальный вектор. Аналогично плоскости ХОZ и УОZ проходят через начало координат(D = 0) и векторы `j =(0, 1, 0) и `i = (1,0,0) – их нормали соответственно.

Если D¹0, то преобразуем общее уравнение так

Ах + Ву +Сz = –D, , .

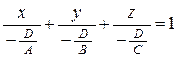Обозначив здесь , , , получим уравнение
, (13)

которое называется уравнением плоскости в отрезках на осях. Здесь а, b, c – величины отрезков, отсекаемых плоскостью на осях координат (рис.). Это уравнение удобно использовать для построения плоскости в системе координат. Нетрудно убедиться, что точки (а, 0, 0), (0. b, 0), (0, 0, с) лежат на плоскости. Прямые, проходящие через эти точки, называются следами плоскости на координатных плоскостях.

Например, построим плоскость

2х – 3у + 4z –12 = 0.

Приведем это уравнение к виду (13), получим

Для построения плоскости в системе координат, отметим на оси ОХ точку (6, 0, 0), на оси ОУ точку (0, -4, 0), на оси ОZ – (0, 0, 3), соединим их отрезками прямы (следы плоскости). Полученный треугольник есть часть искомой плоскости, заключенная между осями координат.

Таким образом, чтобы найти уравнение плоскости, достаточно знать

- либо нормальный вектор этой плоскости и любую ее точку (уравнение (10));

- либо три точки, лежащие на плоскости (уравнение (11)).

Взаимное расположение плоскостейв пространстве удобно изучать с помощью соответствующих им векторов. Если a – плоскость с нормальным вектором `N, то

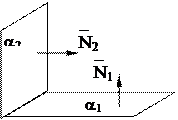· a₁ || a₂ Û `N<sub>1</sub> ||`N₂;

· a₁ ^ a₂ Û `N<sub>1</sub> ^`N₂ ;

· Угол 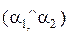между двумя плоскостями равен углу между их нормальными векторами или является смежным к нему, причем .

· Расстояние от точки М₀(х₀, у₀, z₀) до плоскости Ах + Ву + Сz +D = 0 находят по формуле

.

Вывод формулы аналогичен тому, как это было проделано для прямой на плоскости. Провести его самостоятельно.