Определение 4.4.

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний которых до двух заданных точек (фокусов) есть величина постоянная, меньшая, чем расстояние между фокусами.

Если расположить фокусы гиперболы на оси ОХ так, чтобы начало координат оказалось по середине между ними, обозначить расстояние между фокусами 2с, модуль разности расстояний – 2а, 2a > 2с , то символьное уравнение гиперболы будет иметь вид |r₁ – r₂| = 2a, а в координатной форме оно запишется так:

½ – ½= 2а.

Преобразовав это уравнение так же как и в случае эллипса, и обозначив b² = с² – а² , получим каноническое уравнение гиперболы

, (19).

Исследуя форму гиперболу, находим, что

1) кривая симметрична относительно осей и начала координат, поэтому исследование формы достаточно провести для части кривой, расположенной в первой четверти и являющейся графиком функции , х Î [а, +¥);

2) точки пересечения с осью ОХ (–а, 0) и (а, 0) – эти точки называются вершинами гиперболы; с осью ОУ кривая не пересекается;

3) прямые у = 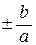– асимптоты гиперболы. При изменении х от а до бесконечности функция возрастает от 0 до бесконечности, т.к. у¢ = > 0 для всех хÎ[a , +¥). Кроме того, эта часть кривой выпуклая: у¢¢ = > 0 при хÎ[a , +¥). Изобразив часть гиперболы в первой четверти в соответствии с этими исследованиями, затем отобразим эту линию симметрично относительно осей и начала координат на остальные четверти, получим искомую гиперболу.

На практике по заданному каноническому уравнению гиперболу строят так.

1. Сначала строят осевой прямоугольник: слева и справа от начала координат на расстоянии а проводят прямые, параллельные оси ОУ, а сверху и снизу на расстоянии b от начала координат – прямые, параллельные оси ОХ.

2. Прямые, на которых лежат диагонали полученного прямоугольника, есть асимптоты гиперболы.

3. Точки пересечения сторон прямоугольника с осью ОХ – вершины гиперболы. От вершин к асимптотам в левой и правой полуплоскости проводят ветви гиперболы.

Точки А(–а, 0) и С(а, 0) называются вершинами гиперболы, точка О (начало координат) – центром гиперболы. Отрезок ОА = ОС = а называется действительной полуосью гиперболы, отрезок ОВ = OD = b – мнимой полуосью. Оси координат при этом так же называют соответственно действительной осью (ее гипербола пересекает в двух точках) и мнимой осью (ее гипербола не пересекает). Расстояния r₁ и r₂ от точки гипербол до фокусов называются фокальными радиусами.

Если фокусы гиперболы расположить на оси ОУ, то ее уравнение будет иметь вид

, или , (20).

где а –мнимая полуось, b – действительная. Гиперболы (2) и (3) называются сопряженными. Они имеют одни и те же асимптоты.

Таким образом, по каноническому уравнению гиперболы легко определить, какая из осей является действительной (та, что входит в уравнение с плюсом), а какая – мнимой (входит с минусом).

Если а = b, гипербола называется равносторонней (равнобочной), ее асимптоты перпендикулярны друг другу.