Определение 4.5.

Параболой называется геометрическое место точек, равноудаленных от заданной точки (фокуса) и от заданной прямой (директрисы).

Найдем уравнение параболы, используя это определение.

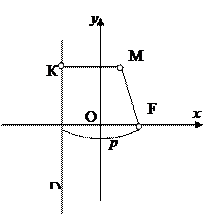Пусть р – расстояние между фокусом F и директрисой D. Расположим систему координат так чтобы директриса была параллельна оси ОУ, фокус находился на оси ОХ, начало координат располагалось посередине между фокусом и директрисой. Пусть М(х, у) –текущая точка параболы, фокус F( 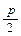,0), уравнение директрисы х = – 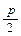, проекция точки М на директрису – точка К(– 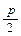, х). Тогда символьное уравнение параболы |FM| = |MK| в координатной форме примет вид

.

После преобразований получаем у² = 2рх.

Если фокус параболы поместить в точку F(– 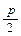, 0), а директрисой взять прямую х = 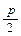, то уравнение приобретет вид у² = –2рх. Поэтому каноническим уравнением параболы называют уравнение вида

у² = 2рх, (21)

где р – параметр произвольного знака.

Исследуем расположение параболы по ее каноническому уравнению (4).

1) Проходит через начало координат (0, 0).

2) Кривая симметрична относительно оси ОХ: точки (х, у) и (х, –у) принадлежат параболе. Ось ОХ при этом называют осью параболы.

3) В силу симметрии исследование достаточно провести при у > 0. Рассмотрим функцию 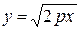, при р > 0 область определения этой функции хÎ[0, +¥); при р < 0 область определения хÎ(–¥, 0]. Производные этой функции равны у¢ = 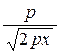, у¢¢= .Для р>0 эта функция возрастает при хÎ(0, +¥), убывает при хÎ(–¥, 0), а в точке (0, 0) имеет минимум. Для р < 0, наоборот, при хÎ(0, +¥) убывает, при хÎ(–¥, 0) возрастает, в точке (0, 0) – максимум. Точу (0, 0) называют вершиной параболы. При р>0 и при у¢¢ < 0, значит, кривая выпуклая.

4) По этим исследованиям вырисовывается следующая кривая

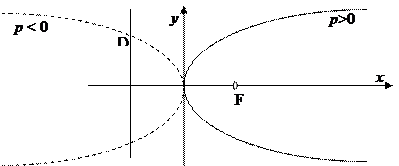Если фокус параболы расположить на оси ОУ, директрису провести параллельно оси ОХ, начало координат расположить по-прежнему посередине между фокусом и директрисой, то получим уравнение параболы в виде

х² = 2ру, (22)

которое также называется каноническим уравнением параболы. Эта парабола имеет вершиной начало координат, осью симметрии ось ОУ; при р >0 ветви параболы направлены вверх, при р < 0 – вниз.