
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямая в пространстве.

Рассмотрим векторное уравнение прямой `r =`r0 + (1), где `r0 – радиус-вектор произвольной фиксированной точки прямой, а `S – направляющий вектор этой прямой (т.е. вектор, параллельный этой прямой). Если М0(х0, у0, z0) и `r0 = (m, n. p), то из (1) имеем
(х, у, z) = (х0, у0, z0) + t(m, n. p),
откуда получим
 , (14)
, (14)
– параметрические уравнения прямой в пространстве. Исключая t из этих уравнений получим
 , (15)
, (15)
– канонические уравнения прямой.
Если известны две точки М1(х1, у1, z1) и М2(х2, у2, z2) прямой, то ее уравнения можно записать в виде
 , (16)
, (16)
– уравнения прямой, проходящей через две заданные точки М1(х1, у1, z1), М2(х2, у2, z2).
Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, поэтому она может быть задана системой двух линейных уравнений – уравнений плоскостей, пересечением которых является:
 . (17)
. (17)
При этом говорят, что заданы общиеуравнения прямой в пространстве.
 Здесь a1: А1х + В1у + C1z + D1 = 0 и a2: А2х + В2у + C2z + D2 = 0 – плоскости, линией пересечения которых является данная прямая l. Заметим, что направляющий вектор `S прямой l ортогонален векторам `N1и`N2 – нормальным векторам плоскостей
Здесь a1: А1х + В1у + C1z + D1 = 0 и a2: А2х + В2у + C2z + D2 = 0 – плоскости, линией пересечения которых является данная прямая l. Заметим, что направляющий вектор `S прямой l ортогонален векторам `N1и`N2 – нормальным векторам плоскостей
Таким образом, чтобы найти уравнения прямой в пространстве, достаточно знать
· либо две ее точки (уравнения (16));
· либо точку и направляющий (параллельный) вектор этой прямой (уравнения 14 или 15);
· либо две плоскости, пересечением которых прямая является (уравнения 17).
Заметим, что из канонических уравнений прямой легко определить пару плоскостей, пересечением которых является данная прямая. Достаточно рассмотреть «парные» равенства, например,
 , откуда получим
, откуда получим 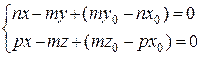
Т.е. прямая представлена как пересечение плоскостей, параллельных осям координат (первая параллельна оси ОZ, вторая – оси ОУ).
Таким образом, от канонических уравнений (или уравнений вида (16)) нетрудно перейти к общим уравнениям прямой в R3.
Наоборот, если по общим уравнениям (17) нужно записать канонические уравнения, то это можно сделать двумя способами:
1) Найти общее решение СЛУ (17) (она всегда совместна и неопределенна, т.к. существует линия пересечения данных плоскостей); по общему найти два произвольных частных решения – две точки искомой прямой; по ним записать уравнение (16) и преобразовать в(15).
2) Найти частное решение СЛУ (17), придав какое-либо значение одной из переменных. Это можно сделать, т.к. система содержит 3 неизвестных и два уравнения, ранг системы равен 2, т.к. плоскости пересекаются, а не совпадают, значит, одна переменная – свободная, ей придаем произвольное значение. Затем найти направляющий вектор`S = `N1´`N2, где `N1и`N2 – нормальные векторы плоскостей, уравнения которых указаны в системе (17). Указанный вектор является направляющим для данной прямой, т.к., по определению от перпендикулярен векторам `N1и`N2. Записать уравнение (15).
Например, найдем канонические уравнения прямой по ее общим уравнениям
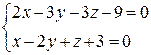 .
.
Положив в этих уравнениях z = 0, получим  , откуда у =15, х =27. Таким образом, точка (27, 15, 0) лежит на данной прямой.
, откуда у =15, х =27. Таким образом, точка (27, 15, 0) лежит на данной прямой.
Найдем `S = `N1´`N2 =  .
.
Таким образом, `S = (-9, -5, -1). Тогда канонические уравнения прямой имеют вид
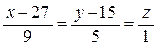
Изучение взаимного расположения прямых и плоскостей в пространстве может быть сведено к изучению взаимного расположения соответствующих этим прямым и плоскостям векторов и точек.
 |
· l1 || l2 Û `S1 || `S2 ;
· 
|
 a || l Û `N ^`S
a || l Û `N ^`S
·  a ^ l Û `N ||`S
a ^ l Û `N ||`S
· 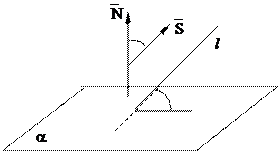 l Î a Û `N ^`S и $ М0Îa, М0Îl.
l Î a Û `N ^`S и $ М0Îa, М0Îl.
· Угол  между прямой и плоскостью равен углу, дополнительному к углу между нормальным вектором `N плоскости a и направляющим вектором `S прямой l, т.е.
между прямой и плоскостью равен углу, дополнительному к углу между нормальным вектором `N плоскости a и направляющим вектором `S прямой l, т.е.  =
= 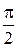 –
– 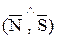
Дата добавления: 2015-04-15; просмотров: 232; Мы поможем в написании вашей работы!; Нарушение авторских прав |