Определение 4.3.

Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Найдем уравнение эллипса. Для этого возьмем систему координат так, чтобы начало координат располагалось по середине между фокусами, ось ОХ проходила через фокусы. Пусть расстояние между фокусами F₁ и F₂ равно 2с, а сумма расстояний от точки М(х, у) эллипса до фокусов равна 2а: r₁ + r₂ = 2a, 2a > 2с.

Тогда фокусы имеют координаты F₁(с, 0) и F₂(–с, 0), расстояния до фокусов равны соответственно

r₁ = , r₂ = .

Отсюда находим уравнение эллипса

+ = 2а

Упрощая уравнение, получим

Полагая здесь а² – с² = b², получим уравнение эллипса

, (18)

которое называется каноническим уравнением эллипса.

Исследуем форму эллипса, используя это уравнение.

1) Нетрудно видеть, что если точка (х, у) принадлежит эллипсу, то ему принадлежат и точки (–х, у), (х, –у) , (–х, –у), т.е. эллипс симметричен относительно осей координат и относительно начала координат.

2) Запишем уравнение (1) в виде откуда следует, что хÎ[–a; a], yÎ [–b, b].

3) В силу симметрии достаточно изучить характер линии при хÎ[0; a].

Когда х растет от 0 до а, 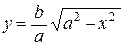убывает от b до 0, т.к. у¢ = < 0 для всех хÎ[0, a). Кроме того, кривая выпуклая: у¢¢ = < 0 при хÎ[0, a).

Учитывая эти исследования, построим график функции 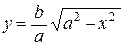при хÎ[0, a] и отразим его симметрично относительно осей координат и начала координат.

Точки А, В, С, D пересечения эллипса с осями координат называются вершинами эллипса, точка О называется центром эллипса, отрезок АО = ОС = а называется большой полуосью, а ОВ = OD = b – малой полуосью эллипса, расстояния r₁ и r₂ от точки эллипса до фокусов называются фокальными радиусами.

Если бы мы расположили фокусы эллипса на оси ОУ, уравнение эллипса имело бы точно такой же вид, как и уравнение (1), только большой полуосью следовало бы считать b. В дальнейшем, договоримся, что большая полуось соответствует оси, на которой лежат фокусы эллипса, и наоборот, из уравнения эллипса по большему параметру а или b можно определить, на какой оси координат лежат фокусы эллипса.

На практике по заданному каноническому уравнению построить эллипс можно так: от начала координат влево и вправо по оси ОХ отложить отрезки длиной а, а по оси ОУ вверх и вниз – отрезки длины b. Через полученные точки-вершины провести правильный овал.

Если а = b = , то с = 0, фокусы эллипса сливаются в одну точку – начало координат – и эллипс вырождается в окружность

х² +у² = а²

с центром в начале координат и радиусом а.