Глава 6. Математический аппарат для описания кибернетического управления: концепция "обратной связи".

Принципы кибернетического управления: положительная и отрицательная обратная связь ("кнут и пряник"). - Линейный случай - модель Мальтуса. - Нелинейная обратная связь - модель Ферхюлста. - Интерпретация и обобщение модели Ферхюлста: "квота вылова" как модель оптимального управления. - Двухкомпонентная модель социально-экономической системы с обратной связью: математическое исследование, экономическая и социальная интерпретации. – Вопросы и задания.

Принципы кибернетического управления: положительная и отрицательная обратная связь ("кнут и пряник").

Итак, управление системой мы можем рассматривать как осуществление переходов между ее состояниями. Но что такое состояние? Это, по определению, нечто устойчивое, - то есть имеется в виду, что параметры, которые его характеризуют, принимают некие стационарные, неизменные во времени значения. Однако каждая система подвергается случайным (или целенаправленным) воздействиям со стороны окружающей среды. В этом случае мы ожидаем, что система, будучи выведенной из определенного (например, равновесного или стационарного) состояния, обладает способностью «самопроизвольно» вернуться к стационарным характеристикам, то есть в рассматриваемое состояние.

А что делать, если система не обладает этим свойством? Чтобы ответить на этот вопрос, зададим встречный: а как же тогда мы можем говорить о «состоянии»? Таким образом, приходим к выводу, что говорить о состоянии для системы имеет смысл только в том случае, когда это состояние является устойчивым. Иными словами, мы ожидаем, что состояние системы должно обладать некими границами устойчивости, то есть что при малом изменении своих параметров (оставаясь все еще внутри границы устойчивости) система останется все в том же состоянии.

Но ведь могут быть ситуации, когда такие границы устойчивости для системы являются «слишком узкими», и нам очень хотелось бы их расширить. Можно ли это сделать, и если можно, то каким образом?

Для того, чтобы ответить на этот вопрос, нужно ввести понятие об «управляющем воздействии». Для того, чтобы описать его, произведем разбиение всего множества параметров, характеризующих систему, на два класса. Первый класс: параметры, на которые мы не можем оказать влияния. Второй класс – это параметры, которые мы можем – в тех или иных пределах – изменять. Вот такие параметры, которые мы можем изменять, и называются управляющими.

Управляющими параметрами называются такие характеристики системы, которые обладают двумя свойствами: во-первых, они могут быть изменены в нужную для нас сторону (например, по величине и знаку) путем внешних по отношению к исследуемой системе воздействий, и, во-вторых, они определяют границы устойчивости системы (в частности – скорость стремления других характеристик системы к своему стационарному значению, которое характеризует данное состояние системы). В общем случае для каждого состояния управляющие параметры будут разными.

Отметим, что мы не связываем управляющие параметры исключительно только с процессом возврата системы к данному состоянию. Определение дано в таком виде, что оно допускает и управление переходом системы к новому состоянию. Например, это возможно, когда границы устойчивости системы (в данном состоянии!) под воздействием внешнего управления сужаются до величины, когда внешние случайные воздействия (факторы) уже выводят систему за эти границы.

Как следует из сделанного выше примечания, мы можем, в общем случае, все способы управления системой разделить на два альтернативных класса.

· Управление, призванное обеспечить устойчивость системы в данном состоянии. Это обеспечивается за счет так называемой отрицательной обратной связи.

· Управление, призванное обеспечить перевод системы из одного состояния в другое. Это достигается за счет положительной обратной связи.

Как организована вообще обратная связь?

Представим себе систему. Пусть она отклонилась от своего текущего состояния. Об этом мы можем судить по изменению значений ряда параметров, которые ее характеризуют. Теперь мы вынуждены принимать решение – то есть определять цель своего управления: способствовать ли возвращению системы в свое первоначальное состояние (отрицательная обратная связь – прилагательное «отрицательная» имеет не только буквальный смысл (это мы увидим ниже!), но и подчеркивает, что мы стремимся уменьшить те изменения, которые внесены окружающей средой), или же наоборот, увеличить это отклонение с тем, чтобы система перешла к новому состоянию (положительная обратная связь: опять прилагательное «положительная» имеет не только буквальный смысл, но также и символический, подчеркивающий наше стремление увеличить имеющие место отклонения в системе).

По сути, положительная и отрицательная обратные связи образуют тем самым контур управления, имеющий замкнутый вид за счет появления возможности дозирования управляющих воздействий и анализа их результатов.

Известно всего два эффективных – и взаимодополняющих! – способа управления людьми в социальных и экономических структурах: это методы «кнута» и «пряника». По сути – они часто трансформируются в методы поощрения и наказания. Это – осуществление все той же самой положительной или отрицательной обратной связи. Поощрение соответствует отрицательной обратной связи, фиксирующей те или иные действия сотрудника, то есть – поощряющие его к продолжению текущей своей деятельности. Теперь мы можем сказать – поощрение стимулирует его нахождение в данном состоянии. Наказание – наоборот: поощряет его изменить свое текущее состояние на другое. Кстати: теперь нам становятся ясными также и причины наличия именно этих двух систем управления отдельным человеком, - это оптимальный набор, позволяющий осуществлять эффективное управление его деятельностью и поведением. Использование только одного из этих методов означает, тем самым, неэффективность управления. В эффективно работающей фирме должны быть четко зафиксированы как способы поощрения, так и способы наказания сотрудников. Конечно, при этом и поощрения, и наказания должны относиться исключительно только к той области, результаты которой зависят от личной деятельности данного сотрудника, - то есть определяются тем состоянием, в котором находится данный сотрудник. Непонимание этого обстоятельства – когда сотрудник наказывается/поощряется не за свои личные действия, приводит к неэффективности управления социальными и экономическими системами.

Линейный случай - модель Мальтуса.

Перейдем теперь к математической форме описания сказанного выше.

Рассмотрим систему, которая характеризуется всего одной характеристикой х – такие системы называются однокомпонентными. Пусть состояние системы характеризуется ее значением х₀. Из-за внешних воздействий характеристика системы изменилась и стала равна х₁. Наиболее простой случай управления – когда мы реализовали такие условия, что скорость изменения координаты оказывается пропорциональной ее отклонению от ее равновесного (стационарного) положения х₀.

Математически это можно записать так:

(6.1)

Удобнее записывать уравнение сразу относительно изменения характеристики – то есть изменения «координаты» системы Dх.

В уравнении (6.1) k – это так называемый управляющий параметр, - в нашем случае число, характеризующее систему и которое мы можем изменять как по величине, так и по знаку – например, сделать его либо положительным, либо отрицательным – при помощи внешних (управляющих) воздействий.

Решение уравнения (6.1) записывается в виде

(6.2)

Здесь х₁ – значение характеристики х (отклонение от равновесия) при t=0, то есть – в начальный момент времени.

Из (6.2) видно, что при k>0 система будет все более удаляться от своего равновесного состояния, характеризуемого значением х₀. Наоборот, при k<0 система будет возвращаться к своему равновесному состоянию. Таким образом, в первом случае – при k>0 – имеет место положительная обратная связь, а при k<0 – отрицательная обратная связь.

Скорость, с которой будет осуществляться это удаление/приближение, зависит от абсолютной величины управляющего параметра – от |k|. Чем больше эта величина, тем быстрее система удаляется/возвращается к равновесному состоянию.

Итак, в рамках этой математической модели мы получаем возможность регулировать – то есть управлять системой посредством:

1. Создания положительной/отрицательной обратной связи.

2. Изменения силы этой обратной связи (величины модуля управляющего параметра |k|).

Примером уравнения (6.1), описывающего реальную социально-экономическую ситуацию, является так называемая модель Мальтуса для численности населения. В ее основу заложено «простое и естественное» предположение: прирост количества людей пропорционален их имеющемуся количеству. В этом случае дифференциальное уравнение, описывающее отклонение системы от некоторого начального количества людей N₀, может быть записано так: dN/dt=kN. Конечно, здесь k>0, чтобы имел место именно прирост, а не убыль населения. Решение этого уравнения имеет вид N(t)=N₀exp(kt), - полагается, что при t=0 численность населения становила N₀. Как видно из решения, численность населения в такой модели стремительно нарастает, - период удвоения количества населения может быть рассчитан по формуле T=ln2/k: по демографическим статистическим данным этот период времени сегодня составляет 40 лет. В модели Мальтуса мы получили рост населения в геометрической прогрессии. Вместе с тем известно, что ресурсы, которыми обладает та или иная страна (да и вся планета в целом!) возрастают в прогрессии арифметической. Но тогда приходим к выводу, что, по мере истечения времени, рост населения происходит быстрее, чем прирост ресурсов! Другими словами, относительное количество ресурсов – количество ресурсов, приходящихся на одного человека – с течением времени будет уменьшаться. В этом, собственно, и состоит вывод теории Мальтуса. Этот вывод был им сделан в начале ХIХ века, а в конце ХХ века к этому же выводу пришли и ученые, сформировавшие неформальную организацию под названием «Римский клуб». Конечно, пришли они к нему, используя гораздо более «изощренные» теоретические и математические модели. Собственно, именно в такой простой модели, которая оказалась на удивление мало чувствительной к последующим уточнениям, и кроются причины все учащающихся призывов к ограничению рождаемости (то есть к уменьшению управляющего параметра k). Конечно, это не решит проблемы – но хотя-бы даст время на принятие решений. Может быть, добиться, чтобы k=0 – хотя бы в масштабах всей планеты? Однако, как легко видеть, это значение является неустойчивым: чуть только k станет положительным – начнется опять рост населения, а чуть только оно станет отрицательным – количество населения начнет уменьшаться. Конечно, это произойдет не сразу – но такая организация управления затрагивает уже все население Земли, и поэтому требует совершено новых способов управления и координации в масштабах всей планеты. Осуществить это сегодня невозможно. Так что же делать?! Прежде всего – изучать эту проблему, строить новые модели, рассматривать новые возможные сценарии развития событий.

Нелинейная обратная связь - модель Ферхюлста.

Выше был описан случай, когда система отклонялась от своего первоначального положения и стремительно удалялась от него, в рамках этой модели, сколь угодно далеко. Однако мы ожидаем – во всяком случае, модели систем строятся как раз из расчета на это – что, рано или поздно, наша система перейдет в новое состояние. Иными словами, теперь перед нами стоит задача о математическом описании перехода системы из одного состояния в другое.

Для построения такой модели зададимся вопросом: а почему вообще возможно «торможение» изменения характеристики системы? Например, это можно сделать следующим образом: как только значение характеристики системы х начнет приближаться к нужному нам новому значению х₂, значение управляющего параметра k должно уменьшаться и достигать нулевого значения при х= х₂.

Другими словами, для описания управления перевода системы в новое состояние, мы должны рассмотреть случай, когда имеется зависимости управляющего параметра от текущих характеристик системы. Как правило, мы получаем при этом нелинейные дифференциальные уравнения.

Например, для уравнения (6.1) его модификация выглядит так:

(6.3)

Простейший случай – это когда k(x)=1-x, и мы получаем уравнение, называемое уравнением Ферхюлста или логистическим уравнением (к такому виду можно привести при помощи преобразования координат любую линейную зависимости управляющего параметра от характеристики системы)

(6.4)

Нетрудно видеть, что это уравнение описывает переход системы из «неустойчивого» состояния х=0 в устойчивое состояние х=1 – рассматриваются только положительные значения х.

В самом общем случае, отклонения от равновесного – то есть от устойчивого состояния – описываются чаще всего в рамках линейного подхода. Если даже и рассматриваются нелинейные добавки, то они полагаются, в определенном смысле, «малыми» по сравнению с линейными членами. Поэтому можно сделать вывод: для управления посредством отрицательной обратной связи достаточно, как правило, линейного описания. Поскольку линейные методы в математике хорошо развиты, поэтому и неудивительно, что основные успехи в кибернетике (особенно – в кибернетике технической) достигнуты именно в области управления системами с целью сохранения их текущего состояния. Вместе с тем в области кибернетики экономической огромное множество задач носит совершенно противоположный характер: необходимо управлять процессом перевода исследуемой системы в то состояние, которое нам нужно. Следовательно, основным объектом изучения в экономической кибернетике являются нелинейные математические модели. Математический аппарат для их исследования весьма сложен, по этой причине и результатов достигнуто не так много. Впрочем, в рамках технической кибернетики для нелинейных задач результатов также достигнуто весьма мало.

Решение уравнения Ферхюлста (6.4) можно записать в виде

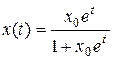(6.5)

Здесь через х₀ обозначено значение характеристики системы в начальный момент времени, при t=0.

Соответствующие решения – называемые интегральными кривыми этого уравнения – изображены на Рис.6.1

Возникает вопрос: а можем ли мы говорить в этом случае о наличии обратной связи вообще? Может быть, было бы более корректно говорить о модели системы? Многое зависит от того, какую задачу мы решаем, то есть от цели нашего исследования. Как правило, вопрос о построении модели системы – это не более чем этап в подготовке и выборе системы управления данным социальным или экономическим объектом. Эта мысль станет боле понятной в том случае, когда уравнение Ферхюлста запишется в размерной форме, - то есть так, как оно обычно и получается при моделировании: dx/dt=ax-bx²=ax(1-bx/a). В такой форме записи явно введены управляющие параметры a и b, посредством изменения которых мы можем управлять как конечным состоянием системы, так и процессом его достижения.

Интерпретация и обобщение модели Ферхюлста: "квота вылова" как модель оптимального управления.

Модель Ферхюлста появилась как простейшее обобщение модели Мальтуса на наличие «естественных ограничений» на рождаемость, приводящих к гибели индивидов. Этой моделью часто описывают размножение биологических объектов разного рода – от бактерий и до высших организмов – таких, как рыбы.

В связи с последним и рассмотрим на примере рыб организацию системы управления их численностью с учетом вылова. Такая задача отражает наше естественное желание использовать ресурс – в данном случае рыбу – для своих нужд. При этом, однако, мы хотим осуществить управление количеством рыб таким образом, чтобы достичь максимально возможного вылова без того, чтобы рыбы исчезли. Таким образом, мы будем рассматривать задачу об оптимальном использовании природного ресурса. При этом под термином оптимальность понимается, что 1) рыбы нужно вылавливать как можно больше, но 2) ресурс не должен истощаться.

Поскольку наше вмешательство является внешним по отношению к системе, уравнение (6.4) нужно модифицировать.

Рассмотрим две простейшие возможности для модификации.

Прежде всего – мы можем отлавливать рыбу с постоянной скоростью, обозначенной с (количество рыб, вылавливаемых в единицу времени, - например, ежегодно). В этом случае уравнение (6.4) примет вид

(6.6)

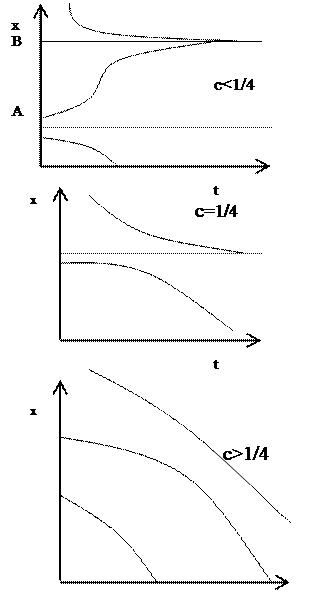
Из уравнения (6.6) следует, что при с>1/4 количество рыб может только уменьшаться, ибо при этом производная будет всегда отрицательна. Другими словами, если мы отлавливаем ежегодно (в качестве естественного промежутка времени удобно выбрать 1 год – время репродуктивного цикла рыб) более чем 25% от стационарно возможного количества рыб (то есть тех, которые были бы без вылова, - в наших обозначениях их количество равно 1), то рыбный ресурс будет истощен, то есть количество рыб устремится к нулю. При 0<c<1/4 – рыбный ресурс установится на некотором уровне, составляющем какую-то часть от максимально возможного х=1. При этом, однако максимальная квота отлова с=1/4 является неустойчивой (любое ее сколь угодно малое превышение приведет к исчезновению системы – рыб), и поэтому должна быть признана недопустимой.

Интегральные кривые уравнения (6.6) показаны на рисунке 6.2.

		t

Может быть, попробуем организовать вылов рыбы по-другому? Например, будем задавать квоту вылова как величину, пропорциональную уже имеющемуся количеству рыбы? Тогда получим уравнение

(6.7)

Здесь величина рх задает скорость отлова рыбы. Из (6.7) очевидно, что имеют место неравенства 0<p<1. При этих условиях в стационарное количество рыб устанавливается на уровне х=В, где В находится как решение уравнения (1-x)x=px. Скорость вылова тогда может быть рассчитана по формуле с=рВ. Зададимся вопросом: когда эта скорость может быть максимальной? Ответ на этот вопрос легче всего найти из геометрических соображений. Точка В находится как пересечение графика квадратичной параболы (1-х)х и прямой рх. Наибольшее значение скорости вылова с=рх равно наибольшей ординате графика функции (1-х)х, а это достигается при х=1/2. При этом значение р=1/2 (необходимо, чтобы значение рх было равно 1/4 - максимальному значению функции (1-х)х, которое достигается при х=1/2. А это достигается, в свою очередь, при р=1/2.

Таким образом, для задачи (6.7) максимальная скорость отлова рыбы устанавливается на уровне с=1/4, - однако теперь, как легко видеть из (6.7), при этом устанавливается устойчивое количество рыбы.

Вот мы и привели пример ситуации, когда рассмотрение разных сценариев управления системой – в нашем случае это были разные сценарии отлова рыбы – позволяет достичь устойчивого перевода системы в новое состояние. Конечно, важные для практики задачи не будут, скорее всего, иметь такой простой вид – однако общая методология их решений будет такой же: сначала подбираем подходящую модель системы и формулируем для нее базовую математическую модель. А потом – исследуем разные способы управления, которые могут быть осуществлены в рамках этой модели. Часто для этого приходится явно выделять те допущения, которые были положены в основу базовой модели и исследовать, можем ли мы от них отказаться – и как при этом изменится математическая модель как системы, так и управления этой системой.

Двухкомпонентная модель социально-экономической системы с обратной связью (обобщение модели Лоттка-Вольтерра): математическое исследование, экономическая и социальная интерпретации.

Выше были рассмотрены примеры однокомпонентных моделей, задающие обратную связи и допускающие внешнее управление. Теперь перейдем к рассмотрению двухкомпонентной модели.

Изложение данной модели ведется на достаточно высоком математическом уровне. Однако именно вследствие этого оно являет собой весьма поучительный пример проведения кибернетического моделирования, которое допускает свое применение к большому количеству самых разных систем. Нас, однако, интересуют прежде всего приложения этой математической модели к социальным и экономическим объектам, и проведение социального и экономического анализа с целью управления такими системами. Весьма важным методологическим обстоятельством является вывод исходной системы уравнений «из общесистемных требований», что как раз наглядно демонстрирует весьма широкий круг возможных приложений полученных результатов. Нелишне также подчеркнуть, что полученные результаты описывают общий случай взаимодействия двух социальных или экономических объектов одного уровня иерархии. Другими словами, если нас интересует задача об описании взаимного влияния двух однородных объектов, или же задача взаимодействия двух компонент, описывающих один и тот же объект – во всех таких случаях мы в качестве базовой придем именно к описанной ниже модели.

Классификация состояний системы.

Вначале рассмотрим общую проблему классификации множества возможных состояний социально-экономических систем – СЭС. Оптимальным языком для такого описания является язык теории множеств и топологии: действительно, каждое состояние есть класс характеристик, который характерен относительно некоторого множества внешних воздействий (например, множества изменений управляющих параметров).

Проведенное ниже описание имеет гораздо более широкие рамки применимости и выходит далеко за рамки задач описания и классификации социальных или экономических систем. В частности, подобные модели широко используются в экологии для описания оптимального управления количеством тех или иных животных или для описания влияния воздействия ядохимикатов на систему связанных между собой трофическими (пищевыми) цепями популяций.

Ниже описана математическая структура, которая является адекватной для проблемы нахождения и классификации всех возможных состояний СЭС. В качестве примера реализации общего подхода рассмотрен случай простейшей для описания динамики СЭС на макроэкономическом уровне. Изложение ведется на "физическом" уровне строгости, однако восстановление точного "математического" уровня описания не представляет, как правило, затруднений.

Рассмотрим следующую математическую структуру (Рис.6.3).

Введем в рассмотрение пространство E всех возможных текущих значений параметров, характеризующих СЭС во всех точках пространства - времени xÎX (город, страна, континент и т.п.). Тогда множество X можно рассматривать как базу, над точками которой при помощи отображения p^-1 восстанавливается некий слой F_xÌE возможных значений параметров СЭС. Переход к иной точке пространства - времени осуществляется при помощи (группового или полугруппового) преобразования gÎG на точках базы g: x®gxÎX. Слой F_x при таком преобразовании переводится в слой F_gx с помощью отображения U_x(g): F_x®F_gxÌE. Заданная конкретная реализация СЭС выделяется некоторой точкой F_iÎF_x и при преобразованиях gÎG на точках базы задает сечение s_i(x).

В математическом смысле описанная структура являет собой пример главного расслоения над базой X, – см., например, книги 1) Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия.- М.:Наука,1979.-760с. и 2) Рохлин В.А., Фукс Д.Б. Начальный курс топологии.-М.:Наука,1977.-488с.

Введем теперь операцию e установления соотношения социально - экономической эквивалентности в пространстве E_s всех орбит сечений s(x). Тогда все возможные состояния СЭС могут быть классифицированы при помощи (частично - упорядоченного) множества - "спектра состояний СЭС", которое эквивалентно фактор - множеству S=E_se.

С учетом вышесказанного моделирование социально - экономических явлений можно производить по следующей схеме:

· Задать пространство E. Его определение должно быть единым (универсальным) и пригодным для широкого класса задач моделирования СЭС.

· Задать оператор p проектирования на базу X (выбор базы, как правило, диктуется спецификой задачи), с помощью которого выделяется слой F_x над данной точкой базы xÎX (это производится с учетом возможности практического определения необходимых параметров).

· Задать группу G, которая будет отражать необходимый уровень пространственно - временного рассмотрения.

· Установить вид отображения U_x(g): F_x®F_gx, где gÎG (в некотором смысле U_x(g) можно назвать оператором "допустимых сценариев").

· Найти оператор выделения сечений s(x) и построить пространство E_s орбит сечений (этот этап по своей сути является чисто математическим и может быть сведен к некоей алгоритмической вычислительной процедуре).

· Ввести соотношение e эквивалентности орбит в пространстве орбит E_s (некоторые предпосылки для выбора соотношения эквивалентности могут быть взяты даже из самой структуры пространства E_s).

· Классификация всех возможных состояний СЭС производится с помощью фактор - множества S=E_se.

В рамках приведенной математической структуры, ориентированной на нахождение спектра состояний СЭС S и на его классификацию однозначный смысл приобретает и термин "процесс" применительно к СЭС, который понимается как переход СЭС от одного состояния к другому.

Рассмотрим пример реализации описанной выше процедуры, который можно назвать моделью взаимодействия "связанных" и "свободных" финансов в замкнутой СЭС. Как уже отмечалось выше, описанные в этом разделе результаты имеют гораздо более широкую область применимости, - однако в целях определенности мы будем вести изложение применительно к СЭС.

Вначале необходимо рассмотреть те особенности, которые связаны с информационной динамикой в СЭС, ибо только в социальной компоненте может произойти "рождение - синтез" новой информации, важной в экономическом плане.

В финансовом отношении проблема "ценности" информации имеет два измерения. Во-первых, в данное количество информации вложено количество финансов, затраченных на ее получение. Конечно, это количество финансов является различным для разных состояний и структур СЭС. Во-вторых, и это главное, эта синтезированная, "экономически - значимая" информация имеет также и независимое финансовое измерение, которое может быть выражено посредством "прибыли" от ее внедрения. Это последнее финансовое измерение также не является инвариантным и зависит от возможностей СЭС по адаптации данной информации и определяется как социальными особенностями (например, наличием специалистов), так и экономическими (например, наличием инфраструктуры, способной перевести эту информацию на технологический уровень, то есть "внедрить" ее). Напомним, что частично эти вопросы были рассмотрены ранее в этой книге, - приложение к экономической ситуации см., например, в главе 5.

Таким образом, финансы имеют также и информационное измерение – «информационную» компоненту, которая сильно связана со спецификой переработки и синтеза информации Человеком, и которая не подчиняется законам сохранения.

В общем случае всю совокупность финансов (ресурсов, денег и т.п. – для краткости будем далее использовать для всего этого комплекса термин «финансы») можно разделить на два основных класса - на "связанные" и "свободные" финансы. Через связанные финансы обозначим ту часть финансов, которая вложена в производство новых финансов (например, в технологии, обучение, создание соответствующих инфраструктур и т.п.) и поэтому уже неспособных к движению. Иными словами, связанные финансы уже "овеществлены" и привязаны к неким материальным объектам и структурам. То есть - эта компонента связана с той информацией, которая как раз сейчас проходит социализацию, - то есть именно с той, которая как раз сейчас переводится в социальный или экономический норматив. Под свободными финансами понимается та их часть, которая подвижна и может быть переведена в связанное состояние (например, путем вложения их в новые технологии). В свободные финансы входит также и "информационная" компонента, которая синтезирована в СЭС вследствие информационной деятельности Человека. Можно сказать и так: свободные финансы это то, что может быть вложено в координаторов (см. главу 10). В качестве ее "финансового измерения" можно взять, например, "среднюю прибыль" при внедрении этой информации с учетом данной структуры СЭС (весьма важным является то обстоятельство, что в разных СЭС (например, в разных государствах) финансовое измерение одной и той же новой синтезированной информации будет разным - например, эта величина возрастает при наличии в СЭС инфраструктур, ориентированных на доводку и внедрение информации.

Вследствие вышесказанного связанные финансы Фⁱ и свободные финансы Ф^c являют собой независимые компоненты финансового поля в макроэкономике: для них, в частности, отсутствует "закон сохранения", то есть Фⁱ_t+ Ф^c_t ¹const.

Замкнутые СЭС.

Теперь можно перейти к реализации общей математической структуры для описания макроэкономических процессов в замкнутой СЭС.

В качестве базы естественным образом выбирается время: X=T. На базе T зададим дискретную группу G (дискретную, например, вследствие естественной дискретизации представления социально - экономической статистики), которую можно отождествить с группой целых чисел Z. Так как в главном расслоении производится отождествление базы и группы, то T=Z. В качестве слоя F_x выбираем прямое произведение Фⁱ_tÄФ^c_t. Тогда для нашей модели E=ФⁱÄФ^cÄT, а p является оператором проектирования на ось T. Оператор U_x(g), переводящий один слой в другой, для нашей модели будет тождественным, что отвечает неизменным "правилам игры".

Оператор, задающий орбиту сечения по заданному "начальному значению" Фⁱ_t=0 и Ф^c_t=0 в общем виде для замкнутой СЭС записывается так (причем имеют место естественные ограничения Фⁱ_t>0 и Ф^c_t>0)

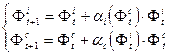(6.8)

Мы рассматриваем пока что социально-экономическую систему в предположении, что она не обменивается с окружающей средой ресурсами, финансами, информацией и т.п. Это, конечно, идеализация – однако она поможет нам провести классификацию состояний исследуемой системы. Фактически, речь сейчас идет о создании базовой модели, которая отражает основные черты и закономерности поведения системы. Впоследствии эту модель мы сможем дополнить – то есть изменить ее так, чтобы учесть интересующие нас эффекты – например, взаимодействие с окружением.

Учет запрета на неограниченное возрастание значений Фⁱ_t и Ф^c_t, а также учет однородности группы T=Z приводит к распределению знаков для (a_i,a_с), показанному на Рис. 6.4 (нетрудно показать, что любой иной простой случай спрямляем к этому типу - см., например, книги 1) Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия.- М.:Наука,1979.-760с. и 2) Рохлин В.А., Фукс Д.Б. Начальный курс топологии.-М.:Наука,1977.-488с.). В безразмерных переменных простейший выбор есть

(6.9)

Здесь b=T_i/T_c -безразмерный период малых колебаний вблизи точки 1=(1,1), а T_i и T_c - характерные "времена нарастания" величин соответственно свободных и связанных финансов вблизи точки 1.

Тогда орбиты являют собой винтовые линии в пространстве E, а пространство орбит E_s взаимно - однозначно проектируется на плоскость (Ф^c, Ф^c) - см. Рис.6.4, где оно естественным образом разбивается на прямую сумму пространств

(6.10)

Таким образом, множество S состоит из двух элементов.

Классификацию орбит можно произвести, например, по их минимальному значению на орбите: Фⁱ_m=min (Фⁱ_t)<1 (для нее одновременно Ф^c_m=min (Ф^c_t)<1), или же - по их периоду (то есть по минимальному времени Т такому, что Фⁱ_t+Т=Фⁱ_t и, соответственно, Фⁱ_t+Т=Фⁱ_t).

Итак, в рамках самой простой модели взаимосвязи свободных и связанных финансов для замкнутой СЭС (то есть в отсутствие ее взаимодействия с окружением) могут реализоваться лишь два ее состояния, причем "типичным" является колебательное состояние. Таким образом, хотя данная модель и крайне огрублена, она тем не менее демонстрирует основные черты динамики макроэкономики СЭС, такие как "периодичность" (то есть - "экономические кризисы") и изменение характеристик состояния СЭС (амплитуды, периода колебаний) в результате как внутренней перестройки (когда "сдвигается" точка 1 - см. ниже), так и при внешних воздействиях (когда происходит перевод системы на иную орбиту - см. Рис.6.4).

Необходимо также отметить, что учет социальных факторов приводит к выделению орбит с Фⁱ_m<Фⁱ_cr<1 (где Фⁱ_cr - некое критическое значение Фⁱ), которые являются "социально опасными" в том смысле, что оставляют слишком малый резерв запаса свободных финансов для парирования внешних воздействий. Интересно, что данный подход позволяет выделить такие "опасные" орбиты еще далеко в "благоприятной области", когда Фⁱ_t>>1 и (или) Ф^с_t>>1, что дает время на принятие предупредительных мер.

Данная модель легко обобщается на более сложные зависимости вторых слагаемых в правой части (6.8). Однако важность этой простой модели состоит в том, что она справедлива всегда для любой замкнутой макроэкономики в "опасной области" - то есть для орбит, далеких от "равновесной точки 1 (см. Рис.6.4) и поэтому представляет несомненный практический интерес.

Поскольку на "каждом обороте" происходит "прибавление" финансов за счет вновь синтезированных, происходит своеобразная "раскрутка" системы - переход ее на "удаленные" орбиты. Настоящая модель дает возможность построить управление СЭС таким образом, чтобы удерживать ее все время в "неопасных" состояниях. Отметим, что связанные и свободные финансы в сумме не дают всей финансовой мощи государства: связанные финансы есть просто часть денег, которые вложены в новые (!) - лишь только в новые - технологии. Кроме того, в дальнейшем следует учесть наличие "разного времени оборачивается" - то есть того обстоятельства, что "разные задачи лежат на разных орбитах" (и имеют разные времена социализации). однако все это можно сделать в рамках развитого здесь подхода.

Перейдем к рассмотрению незамкнутых СЭС.

В общем случае внешнее воздействие на СЭС распадается на два предельных класса: когда t>>Т₀ и когда t<<Т₀, где t - характерное время внешнего воздействия, а Т₀ - период для данной орбиты СЭС.

Рассмотрим случай постоянных внешних воздействий - t>>Т₀ (противоположный случай рассмотрен в следующем пункте). Перейдем также к непрерывным координатам, что позволит применять при исследовании методы качественной теории динамических систем на плоскости (см., например Баутин Н.Н., Леонтович Е.Л. Методы и приемы качественного исследования динамических систем на плоскости.-М.:Наука,1976.-496с.).

Итак, уравнения (6.8) - (6.9) для открытой СЭС при постоянном внешнем воздействии примут вид

(6.11)

Особые точки получаются приравниванием к нулю правой части (4), и для них находим

(6.12)

Здесь обозначено b=db.

Чтобы проследить тенденцию, рассмотрим случай, когда ½a½,½b½<<1. Тогда в первом порядке

(6.13)

Исследование точек 1 и 2 свидетельствует о следующем:

· при a>b точка 1 есть неустойчивый фокус, а 2 - седло; поведение фазовых траекторий (проекций орбит) показано на Рис. 6.5.

· при a<b точка 1 есть устойчивый фокус, а 2 - седло, см. Рис. 6.6.

Социально - экономическая интерпретация.

Значения a>0 соответствуют постоянному оттоку свободных финансов из СЭС, что может выражаться, например, в виде так называемой "утечки мозгов" или же вывозу свободного капитала (или же - невывозу капиталов, полученных за экспорт). Значения b>0 соответствуют притоку сторонних связанных финансов - например, товаров или вкладу сторонних капиталов в связанное состояние в данной СЭС.

Таким образом, случай a>0 и b>0 соответствует "экономически слабой" СЭС. Для нее точка 1 сдвигается в сторону меньших средних уровней как свободных, так и связанных финансов по сравнению с замкнутой СЭС. (Здесь, конечно, следует рассмотреть вопрос о том, а "стоит ли открываться" - следует ли данной стране сейчас "открывать" свою экономику?) Однако при внешнем воздействии изменяется и устойчивость поведения СЭС: "нейтральный" центр переходит в устойчивый или неустойчивый фокус.

Поведение же СЭС при этом распадается на два сценария.

Первый сценарий реализуется при условии, когда ввоз связанных финансов превышает вывоз свободных, то есть когда внешние капиталовложения в экономику страны и ввоз товаров превышают финансовый эквивалент "утечки мозгов" из страны и вывоз капиталов. Тогда СЭС почти из всех начальных состояний приходит к устойчивому состоянию 1, причем с течением времени "амплитуда кризисов" уменьшается - см. Рис. 6.6. Итак, связанные финансы (капиталы) = вложенные "в дело" (в социализацию информации), а свободные финансы - это уже синтезированная информация, готовая к социализации - ждущая своей "очереди" на социализацию.

К сожалению, чаще реализуется второй сценарий, при противоположном соотношении между величинами вывоза свободных финансов и ввоза связанных финансов, когда почти для всех начальных условий наступает полная деградация и уничтожение СЭС путем полного исчезновения либо связанных, либо свободных финансов (см. Рис.6.5). В реальном случае, конечно, при таком сценарии СЭС либо распадается, либо ее распаду помешают такие социальные явления, как диктатуры и войны.

Интересно отметить, что "утечка мозгов" уменьшает средний уровень связанных финансов, что согласуется с "наивной" точкой зрения - "меньше специалистов для внедрения новых технологий". А ввоз чужих капиталов уменьшает средний уровень свободных финансов - ибо "уменьшается выпуск специалистов, способных придумать новые технологии".

Фактически, проанализированный выше случай соответствует внешней экспансии, социально - экономической "атаке" на "слаборазвитую" СЭС. Однако эти же два сценария поведения могут быть реализованы и для "экономически развитых" СЭС, практикующих "ввоз мозгов" и вывоз связанных финансов. В рамках модели (6.11) этому случаю соответствуют отрицательные значения a и b. Случай превышения притока свободных финансов (например, при "ввозе мозгов") над вывозом связанных финансов стабилизирует "развитые" СЭС (см. Рис.6.6). В противном случае СЭС деградирует - и это несмотря на то, что по "внешним признакам" она еще некоторое время может считаться "развитой".

Случай a>0 и b<0 наиболее трагичен - он всегда ведет к деградации СЭС (см. Рис.6.5).

Наконец отметим, что для характерного времени "стабилизации" с состоянию 1 (или же - для характерного времени деградации СЭС) может быть получена оценка как T_c~½a-b½^-1.

Следствия для посткоммунистических стран (Украина, Россия).

Остановимся на некоторых следствиях для посткоммунистических СЭС. Для них характерно, что средний уровень свободных финансов много меньше среднего уровня связанных финансов, или в размерном виде Фⁱ<<Ф^с. Это является следствием того обстоятельства, что в коммунистических режимах практически полностью отсутствовала инфраструктура для внедрения новой экономически - значимой информации. Поэтому для коммунистического режима a>0 и b<0, а динамика СЭС всегда соответствует Рис.6.5. Относительную стабильность таким СЭС мог придать лишь все увеличивающийся вывоз связанных финансов - чаще всего в виде сырья.

Таким образом, главной задачей посткоммунистических СЭС на макроэкономическом уровне является проблема увеличения среднего уровня Фⁱ и уменьшение амплитуды колебаний, то есть сдвиг "вправо" точки 1 (см. Рис.6.4-6.6). Осуществить это лишь путем постоянного воздействия со стороны окружающего мира не представляется возможным: как видно из (6.13), для этого необходимо увеличение вывоза связанных финансов (например, товаров), то есть b<0, что затруднено в силу экономической отсталости страны. Но к тому же при наступлении открытости таких обществ возникает интенсивная "утечка мозгов" (в виде либо физическом, либо информационном), и становится a>0, а тогда деструктивные процессы лишь усиливаются.

Поэтому остается лишь одна возможность: путем перестройки внутренней структуры СЭС, прежде всего в направлении создания инфраструктуры для создания (синтеза) и внедрения новой экономически - значимой информации. Даже внешняя финансовая помощь должна идти не на увеличение доли свободных или связанных финансов (соответственно "без условная" помощь и "целевое финансирование" программ), а лишь на структурную перестройку СЭС. Действительно, "кратковременная" внешняя финансовая поддержка может лишь перевести СЭС на иную орбиту (лучший вариант показан на Рис.6.4: переход s₃®s₂, когда СЭС находится в состоянии А; страна - "донор" при этом должна находиться в состоянии В и осуществить указанный стрелкой переход, чтобы не усугубить свое собственное положение).

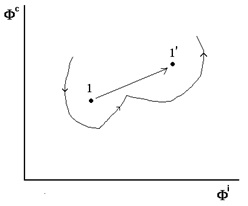
Перестройку структуры СЭС можно производить по двум сценариям (Рис.6.7а,б). Либо "быстрым рывком" (Рис.6.7а), либо медленным "дрейфом" (Рис.6.7б) осуществлять перевод средних уровней 1®1¹. Первый сценарий соответствует так называемой "шоковой терапии" (и требует существенных кратковременных финансовых вливаний в экономику страны), второй - "китайскому варианту". Отметим при этом, что "шоковый" сценарий требует быстрой структурной перестройки СЭС.

Математически изоморфные модели.Рассмотренная здесь модель макроэкономики СЭС изоморфна известной в популяционной экологии модели "хищник - жертва" для взаимодействующих популяций. Эта модель довольно подробно исследована в математическом плане (см, например, Свирежев Ю.М. Нелинейные волны, диссипативные структуры и катастрофы в экологии.-М.:Наука,1987.-368с.), и многие математические выводы сохраняются также и для СЭС. Аналогия между процессами в социально - экономических и экологических системах имеет ярко выраженный практический интерес: она позволяет производить экспериментальное моделирование макроэкономических процессов посредством интерпретации экологических данных.

Некоторые итоги.

Подведем основные выводы из приведенного выше:

A) Предложена математическая структура, ориентированная на нахождение спектра всех возможных состояний социально - экономической системы, а также позволяющая корректно определить сам термин "состояние СЭС".

B) Способность Человека производить - синтезировать новую экономически - значимую информацию делает возможным придать ей финансовое выражение, а также разделить всю массу финансов на "связанные" и "свободные", причем информационная компонента включена в последнюю.

C) Простейший вариант взаимодействия связанных и свободных финансов в замкнутой СЭС задается соотношениями (6.8) - (6.9) безотносительно к конкретной природе и свойствам этих понятий. В этом смысле такое взаимодействие является универсальным и "единственно возможным".

D) Модели (6.8) - (6.9) и (6.11) корректно описывают основные макроэкономические явления в СЭС, включая проблемы, связанные с устойчивостью СЭС, а также выходом СЭС из посткоммунистического состояния.

E) Важнейшее значение для динамики и устойчивости СЭС имеет наличие и особенности функционирования социально - экономических структур, направленных на появление (синтез) новой экономически - значимой информации и на ее адаптацию и "внедрение" на уровне практики экономической деятельности СЭС. Для посткоммунистических СЭС формирование такой инфраструктуры имеет критическое значение.

Наконец, отметим следующее:

· Трех - и более компонентные модели (например, - несколько отраслей экономики, несколько объектов социально - экономического процесса, несколько партий) с запретом на "инфинитные траектории" могут уже демонстрировать поведение типа так называемого "странного аттрактора", то есть - обладать стохастическим свойствами, что резко снижает уровень прогнозируемости развития таких систем (см., например, книгу Пригожин И., Николис Г. Познание сложного. Введение.-М.:Мир,1990.-344с.).

· Управление такими системами состоит либо в сохранении, либо в изменении шумовых свойств таких "траекторий" (соответствующих распределений вероятности, размерности аттрактора, корреляционных функций, показателей Ляпунова, f^-b - шума и т.п.).

· Моделирование такого "рынка" - это создание (или изменение существующих) таких аналоговых (например, - электронных) систем, которые проявляют те же самые шумовые свойства.

Область применения изложенной базовой модели.

Описанная выше модель имеет значительно более широкую область приложений, чем описание связанных и свободных финансов.

Этой моделью - или ее вариантами - описывается взаимодействие вообще между любыми двумя КС, принадлежащими к одному и тому же уровню иерархии. Действительно: пусть одна КС характеризуется параметром Фⁱ, а другая - параметром Ф^c. Тогда математическая модель для взаимодействия этих параметров имеет вид (6.8), а ее простейшая реализация - (6.8) и (7.9) (или (6.10) - при учете взаимодействия этих двух КС с окружающей средой).

Таким образом, моделями (6.8) - (6.10) могут быть описаны многие из сторон социальной и экономической активности Человека. В частности, - взаимодействие между двумя партиями или же двумя "общественными мнениями" ( и тогда Фⁱ и Ф^c - это, например, количество людей, придерживающихся соответствующих взглядов или точек зрения) - явление, известное в политологии как "эффект маятника".

Интересно, что наличие в стране 3-х или более "влиятельных" социальных групп (партий, социальных движений и т.п.), как следует из предыдущего пункта, уже не позволяет осуществить надежный политический прогноз и организовать "упорядоченную" передачу власти от одной партии к другой. Вероятно, что это может служить объяснением того, по какой причине в большинстве экономически развитых - и прогнозируемых! - стран мира имеется всего две основные социальные или политические силы ("правящая" и "оппозиционная" группировки), которые периодически сменяют друг друга у власти - по мере того, как они полностью реализуют свою социальную и/или экономическую Программу (или же - по мере того, как будет самой жизнью доказана ее бесперспективность).

Вопросы.

1. Сформулируйте Ваше собственное определение управляющих параметров. Приведите примеры управляющих параметров для разных а) социальных и б) экономических систем.

2. Что такое положительная и отрицательная обратная связи? Сформулируйте Ваше собственное определение этих понятий. Приведите примеры этих связей для а) социальных и б) экономических систем.

3. Приведите примеры социальных и экономических задач, где необходимо при помощи управления обеспечить а) устойчивость системы (объекта, процесса, и т.п.) и б) перевод системы (объекта, процесса, и т.п.) в новое состояние. Опишите, как бы Вы добивались поставленной цели.

4. Приведите примеры а) социальных и б) экономических систем (объектов, процессов, и т.п.), для которых справедлива модель линейной обратной связи (модель Мальтуса). Каким образом Вы предлагаете в рамках приведенных Вами примеров осуществлять управление параметром k?

5. Приведите примеры а) социальных и б) экономических систем (объектов, процессов, и т.п.), для которых будет справедлива нелинейная обратная связь (модель Ферхюлста). Опишите, как Вы предлагаете осуществлять изменение управляющих параметров.

6. Приведите примеры а) социальных и б) экономических систем (объектов, процессов, задач и т.п.), для которых характерны двухкомпонентные модели. Опишите, какие именно характеристики является компонентами для каждого из случаев.

7. Опишите в рамках двухкомпонентной модели процесс взаимодействия двух политических партий. Проведите интерпретацию полученных в тексте результатов для этого случая.

8. Опишите в рамках двухкомпонентной модели процесс «борьбы за рынок» двух конкурирующих между собой фирм. Проведите интерпретацию полученных в тексте результатов для этого случая.

Задачи.

1. Решите уравнения (6.1), (6.4), (6.6) и (6.7) методом разделения переменных. Объясните, почему для последних трех уравнений применить операторный метод не представляется возможным.

2. Получите стационарное решение уравнения (6.11) – то есть получите соотношения (6.12). покажите, что при малых значениях управляющих параметров a и b справедливы соотношения (6.13).

3. Опишите процесс взаимодействия банка и производственного предприятия в рамках двухкомпонентной модели. Проведите интерпретацию полученных в тексте результатов для этого конкретного случая. Вы получите не только инновационную модель развития региона, но также и объяснение природы инновационных циклов развития той или иной отрасли.