Векторный способ задания движения точки. Векторный способ задания движения точки

I. К И Н Е М А Т И К А

Кинематика точки

Векторный способ задания движения точки

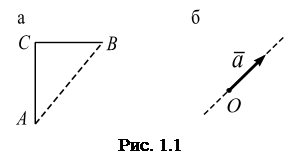
Векторы.Многие физические величины характеризуются одним параметром – модулем этой величины. Например, известно расстояние, которое проходит пешеход (допустим, он прошел 37 км) – при этом не учитывается направление, в котором он путешествовал. Такие величины называются скалярными.Бывают обстоятельства, когда необходимо знать и модуль, и направление физической величины. Например, если пункт А находится в 14 км к востоку от пункта В, то недостаточно направить пешехода, указав расстояние в 14 км для того, чтобы он достиг пункт В. Необходимо определить направление движения. Комбинация величины (модуля) и направления перемещения называется векторной величиной, или просто вектором. Важность понимания различий между векторными и скалярными величинами состоит в том, что для этих величин разные правила сложения, вычитания и умножения. Для скалярных величин эти правила прописаны в алгебре, а для векторных величин – в векторной алгебре. Например, полное расстояние между пунктами А и В вычисляется сложением (рис. 1.1, а), а полное перемещениевычисляется расстояниеммежду пунктами А и В, т.еравно .

Вектор всегда изображается направленным отрезком, длина которого в некотором масштабе равна модулю представляемой вектором физической величины, а стрелка показывает ее направление (рис. 1.1, б). Вектор обозначается буквой со стрелкой над ней, например, ускорение .Точку А называют точкой приложения вектора, а прямую, вдоль которой направлен вектор, называют линией действия вектора.

Проекция силы на ось. Изобразим на плоскости вектор (рис. 1.2). Опустим перпендикуляры из начала А и конца В вектора на оси и , получим отрезки и , называемые проекциями вектора на оси и . Проекции вектора на прямоугольные оси и его модуль и направление вычисляются по формулам:

, , .

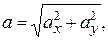
Проекция вектора на ось является скалярной величиной, потому что не имеет собственного направления, а определяется направлением оси (рис. 1.3). Проекция силы будет положительной, если направление вектора силы составляет с положительным направлением оси острый угол – , и отрицательной, если угол тупой – .

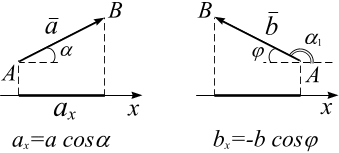
Рис. 1.3

В механике разделяют три типа векторов: свободный, скользящий и связанный.

Свободными векторами представляются физические величины, не изменяющиеся при переходе от одной точки пространства к любой другой. Такие векторы характеризуют физические величины во всем исследуемом пространстве.

Скользящие векторы представляют собой векторные физические величины, остающиеся неизменными вдоль линии действия вектора. Они изменяются при переходе к другой точке пространства, не лежащей на линии действия.

Закрепленные векторы представляют собой векторные физические величины только в данной точке пространства. В других точках пространства они либо имеют другое значение, либо вообще теряют смысл.

Радиус-вектор.Положение точки в пространстве удобно характеризовать радиус-вектором . При изменении конец радиус-вектора опишет кривую в пространстве (рис.1.4, а). Эта кривая называется годографом радиус-вектора и является траекторией движущейся точки.

а

б

Рис. 1.4

Если радиус-вектор разложить по базисным векторам , в плоской прямоугольной системе координат, то (рис.1.4, б):

,

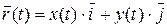где являются координатами радиус-вектора в прямоугольной системе координат.

Модуль радиус-вектора вычисляется согласно теореме Пифагора: 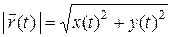. Направление радиус-вектора вычисляется по направляющему косинусу:

Уравнение движения точки, заданное векторным способом.Уравнение движения при векторном способе задания движения задается радиус- вектором этой точки:

.

Скорость точки. Мгновенная скорость точки 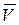в момент времени :

(м/с).

Ускорение точки.Ускорение точки в момент времени :

(м/с²).

Задача 1.1. Движение точки задано радиус-вектором:

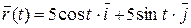(см).

Построить траекторию движущейся точки и вычислить ее скорость при 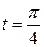с.

Решение. Построить траекторию движущейся точки – это значит построить годограф радиус-вектора. Для построения годографа составим таблицу точек годографа для отдельных значений t.

Таблица 1

t

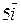
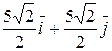
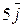
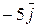
Для любой точки годографа имеем:

, .

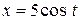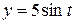Возведем эти уравнения в квадрат и, сложив между собой, получим, что при любом t выполняется равенство , т.е. все точки годографа лежат на окружности радиусом 5 см, следовательно, траекторией является окружность радиусом см (рис. 1.5).

Вычислим вектор скорости:

.

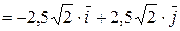Ответ: траекторией является окружность радиусом см; скорость точки .