Скорость

Скорость любой точки тела (например, точки В) при его плоском (плоскопараллельном) движении геометрически складывается из скорости полюса и скорости точки В в её вращении вместе с телом вокруг полюса А:

.

В полученном равенстве – скорость полюса, – скорость точки В, которую она получает при вращении тела вокруг полюса А:

, .

Задача 4.1. Диск радиусом R катится без скольжения по линейному рельсу. Центр С диска движется согласно уравнению . Вычислить скорости точек обода диска Р, М, , N, расположенных, как показано на рис. 4.3.

Решение. Получим уравнения движения диска. Имеем (рис. 4.3, а):

, , .

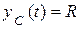а		б
Рис. 4.3

За полюс выберем точку . Вычислим скорость полюса и угловую скорость вращения диска вокруг полюса Имеем:

, ,

; .

Применим к точке Р колеса теорему о скоростях при плоском движении:

.

Отметим, что , .

Так как векторы и лежат на одной прямой (рис. 4.3, б), имеем:

.

Отметим, что скорости точек, лежащих на ободе диска, по модулю равны между собой, т.к. лежат на одном расстоянии от полюса:

.

Вычислим скорость точки (рис. 4.3, б):

,

здесь 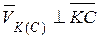, и :

.

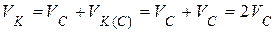Вычислим скорость точки М:

здесь , :

.

Направление скорости находим построением параллелограмма (рис. 4.3, б). Вычисляем скорость точки N:

Здесь: , :

.

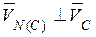Направление векторов скоростей и находим построением соответствующих параллелограммов (рис. 4.3, б).

Отметим, что перпендикуляры, проведенные к скоростям в точках М, , N, пересекутся в точке , скорость которой равна нулю.

Ответ: ; ; ; .