
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм решения
При решении задач на вычисление уравнений движения плоского твердого тела и вычисление скоростей точек, жестко связанных с плоской фигурой, рекомендуется такая последовательность действий:
· выбираем неподвижную систему координат и точку С (полюс), жестко связанную с плоской фигурой;
· составляем уравнения движения плоской фигуры: определяем координаты полюса относительно неподвижной системы координат  ,
,  ; проводим через точку C прямую, определяем угол
; проводим через точку C прямую, определяем угол  , который эта прямая составляет с горизонтальной неподвижной осью;
, который эта прямая составляет с горизонтальной неподвижной осью;
· вычисляем скорость полюса 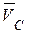 и скорость любой точки тела (например, точки В), как точки, мгновенно вращающейся вокруг полюса -
и скорость любой точки тела (например, точки В), как точки, мгновенно вращающейся вокруг полюса - 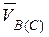 ;
;
· вычисляем скорость любой точки, жестко связанной с телом (движущейся вместе с полюсом и вращающейся вокруг полюса), по теореме о скоростях точек тела при его плоскопараллельном движении:  .
.
Если определить  аналитически сложно, находим мгновенный центр скоростей для заданного положения твердого тела, восставляя перпендикуляры к векторам скоростей двух точек плоской фигуры (точки В и С, направление вектора скорости в точках С и В известно), и определяем мгновенную угловую скорость фигуры.
аналитически сложно, находим мгновенный центр скоростей для заданного положения твердого тела, восставляя перпендикуляры к векторам скоростей двух точек плоской фигуры (точки В и С, направление вектора скорости в точках С и В известно), и определяем мгновенную угловую скорость фигуры.
J 
| Задачи для самостоятельного решения | ||||||||||

| 1. В механизме длина кривошипа  см, см, 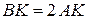 . Вращение кривошипа ОА равномерное, . Вращение кривошипа ОА равномерное,  с-1. Для заданного положения механизма вычислить: с-1. Для заданного положения механизма вычислить: 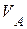 , , 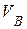 , , 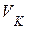 , ,  , ,  , ,  . .
| ||||||||||
2. В кривошипно-шатунном механизме кривошип  см вращается равномерно с см вращается равномерно с  с-1; длина шатуна с-1; длина шатуна  м. Вычислить угловую скорость м. Вычислить угловую скорость  шатуна; скорость его середины М при четырех положениях кривошипа, когда угол ВАО составит 0, шатуна; скорость его середины М при четырех положениях кривошипа, когда угол ВАО составит 0,  , ,  и и  ; ускорение ; ускорение  при вертикальном положении кривошипа ОА. при вертикальном положении кривошипа ОА.

| |||||||||||

| 3. Шестерёнка радиусом 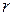 , катящаяся по неподвижной окружности радиусом , катящаяся по неподвижной окружности радиусом  , приводится в движение кривошипом , приводится в движение кривошипом  , вращающимся равноускоренно с угловым ускорением , вращающимся равноускоренно с угловым ускорением 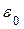 вокруг неподвижной оси вокруг неподвижной оси  . Составить уравнения движения подвижной шестерёнки, приняв за полюс её центр . Составить уравнения движения подвижной шестерёнки, приняв за полюс её центр 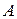 , если при , если при  угловая скорость кривошипа угловая скорость кривошипа  и угол поворота и угол поворота  . .
| ||||||||||
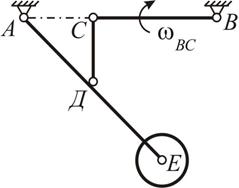
| 4. На чертеже изображена схема убирающегося шасси самолета;  м, м,  м, м,  м, м, 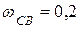 с-1. В данный момент АСВ – горизонтальная прямая, с-1. В данный момент АСВ – горизонтальная прямая,  м.
Вычислить при данном положении механизма скорости точек Д, Е и С; ускорение точки Е. м.
Вычислить при данном положении механизма скорости точек Д, Е и С; ускорение точки Е.
| ||||||||||

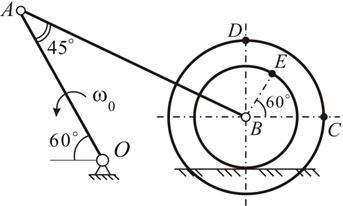
| 5. Кривошип ОА равномерно вращается с угловой скоростью  с-1, приводя в движение шатун АВ. Колесо 1 катится без скольжения по неподвижному колесу 2, радиусы обоих колес одинаковые. Вычислить угловую скорость колеса 1 - с-1, приводя в движение шатун АВ. Колесо 1 катится без скольжения по неподвижному колесу 2, радиусы обоих колес одинаковые. Вычислить угловую скорость колеса 1 -  - и кривошипа - и кривошипа  , имеющего ось вращения, проходящую через центр неподвижного колеса; ускорение точки Д – , имеющего ось вращения, проходящую через центр неподвижного колеса; ускорение точки Д –  , если , если  см. см.
| ||||||||||
6. Колесо радиусом  см, катящееся без скольжения по неподвижному колесу радиусом см, катящееся без скольжения по неподвижному колесу радиусом  см, приводится в движение кривошипом ОА, который вращается с угловой скоростью см, приводится в движение кривошипом ОА, который вращается с угловой скоростью 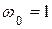 с-1. В свою очередь подвижное колесо приводит в движение шатун с-1. В свою очередь подвижное колесо приводит в движение шатун  см. Вычислить при данном положении механизма скорость точки В, угловую скорость шатуна ВС, скорость ползуна С, угловое ускорение стержня ВС. см. Вычислить при данном положении механизма скорость точки В, угловую скорость шатуна ВС, скорость ползуна С, угловое ускорение стержня ВС.

| |||||||||||
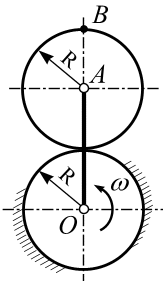
| 7. Диск радиусом  см, катящийся без скольжения по неподвижному диску того же радиуса, приводится в движение кривошипом ОА, который вращается вокруг оси О с угловой скоростью см, катящийся без скольжения по неподвижному диску того же радиуса, приводится в движение кривошипом ОА, который вращается вокруг оси О с угловой скоростью 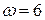 с-1. Найти скорость и ускорение точки В, а также угловое ускорение катящегося диска. с-1. Найти скорость и ускорение точки В, а также угловое ускорение катящегося диска.
| ||||||||||
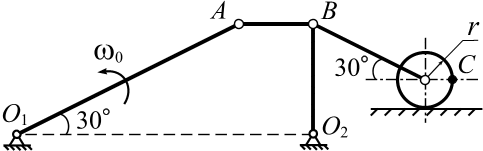
8. В механизме, изображенном на чертеже, вычислить скорости точек А, В, 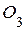 , С, а также угловые скорости всех звеньев и угловое ускорение колеса: , С, а также угловые скорости всех звеньев и угловое ускорение колеса:  см; см;  см; см; 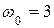 с-1, с-1,  см; колесо катится без скольжения. см; колесо катится без скольжения.
| |||||||||||

| 9. Колесо 1 радиусом 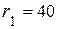 см, катящееся без скольжения по внутренней поверхности неподвижного колеса 2 радиусом см, катящееся без скольжения по внутренней поверхности неподвижного колеса 2 радиусом 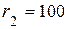 см, приводится в движение кривошипом см, приводится в движение кривошипом  см, который вращается с постоянной угловой скоростью см, который вращается с постоянной угловой скоростью  с-1. с-1.
| ||||||||||
На одну ось О с кривошипом ОА свободно насажено колесо 3 радиусом 20 см, находящееся во внешнем зацеплении с колесом 1. Вычислить угловую скорость  колеса 3, скорость и ускорение точки для указанного положения механизма АВ колеса 3, скорость и ускорение точки для указанного положения механизма АВ 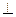 ОА. ОА.
| |||||||||||
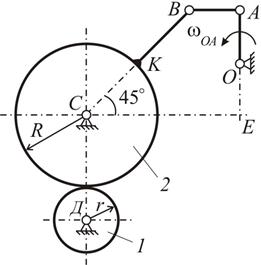
| 10. Две шестеренки находятся во внешнем зацеплении и приводятся во вращательное движение с помощью кривошипа 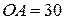 см. Стержень BK жестко соединен с шестеренкой 2. При данном положении механизма вычислить скорость точки B, угловую скорость см. Стержень BK жестко соединен с шестеренкой 2. При данном положении механизма вычислить скорость точки B, угловую скорость  и угловое ускорение и угловое ускорение  шестеренки 1.
Дано: шестеренки 1.
Дано:  с-1; с-1;  ; ; 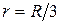 ; ; 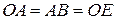 см. Точки С, К и В лежат на одной прямой. см. Точки С, К и В лежат на одной прямой.
| ||||||||||
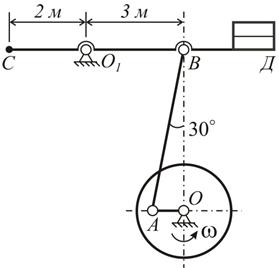
| 11. На чертеже изображена схема механизма станка-качалки нефтяного насоса. Колесо вращается вокруг оси О, делая 20 об/мин. Для указанного на чертеже положения балансир СД – горизонтален, шарнир А и точка О на одной прямой,  см.
Вычислить: см.
Вычислить: 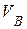 , ,  , ,  , ,  . .
| ||||||||||
12. Колесо радиусом 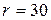 см катится по горизонтальному рельсу. Центр колеса движется согласно уравнению см катится по горизонтальному рельсу. Центр колеса движется согласно уравнению  (см). К колесу кольцом А прикреплен стержень АВ, конец которого скользит по рельсу. Указанное на чертеже положение соответствует (см). К колесу кольцом А прикреплен стержень АВ, конец которого скользит по рельсу. Указанное на чертеже положение соответствует 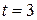 c. Вычислить для этого положения c. Вычислить для этого положения 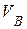 , , 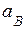 . .

| |||||||||||

| 13. На чертеже изображен кривошипный механизм с ножной педалью. В данный момент  , ,  , шатун вертикален; , шатун вертикален;  с-1, с-1, 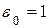 с-2, с-2, 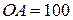 см, см,  см, см,  см.
Для указанного на чертеже положения механизма вычислить: см.
Для указанного на чертеже положения механизма вычислить:  , , 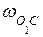 , ,  . .
| ||||||||||
14. Вычислить скорость 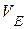 поршня поршня  и ускорение и ускорение 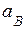 приводного механизма насоса в положении, указанном на рисунке, если приводного механизма насоса в положении, указанном на рисунке, если  20 см, 20 см,  . Вращение кривошипа . Вращение кривошипа 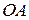 равномерное, с угловой скоростью равномерное, с угловой скоростью  с-1. с-1.

| |||||||||||
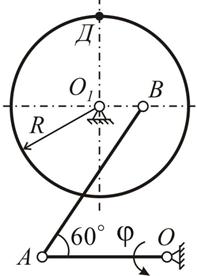
| 15. Точильный станок приводится в движение педалью 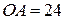 см, которая колеблется около оси: см, которая колеблется около оси:  (рад) (угол (рад) (угол 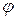 отсчитывается от горизонтали). Точильный камень вращается вокруг оси отсчитывается от горизонтали). Точильный камень вращается вокруг оси  с помощью шатуна АВ.
Дано: с помощью шатуна АВ.
Дано: 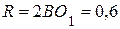 м; м; 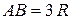 . В момент времени . В момент времени 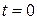 вычислить вычислить 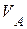 , , 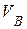 , ,  , ,  . .
| ||||||||||

| 16. На фигуре изображена схема ручного насоса. Рукоятка ОВ вращается с постоянной угловой скоростью  (1/cек). Вычислить скорость точки С в указанном на чертеже положении и угловую скорость звена ВС, когда (1/cек). Вычислить скорость точки С в указанном на чертеже положении и угловую скорость звена ВС, когда  , , 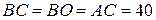 см.
Вычислить также ускорение точки С и угловую скорость шатуна ВА - см.
Вычислить также ускорение точки С и угловую скорость шатуна ВА -  . .
| ||||||||||

| 17. При заданном положении шарнирного механизма 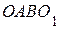 угловая скорость и угловое ускорение звена ОА равны соответственно угловая скорость и угловое ускорение звена ОА равны соответственно  с-1, с-1,  с-2. с-2.  м.
Вычислить в положении, указанном на рисунке, м.
Вычислить в положении, указанном на рисунке, 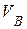 , ,  . .
| ||||||||||

| 18. Кривошип  см вращается с угловой скоростью см вращается с угловой скоростью  с-1 и приводит в движение колесо радиусом с-1 и приводит в движение колесо радиусом  см, которое катится по неподвижной криволинейной поверхности радиусом см, которое катится по неподвижной криволинейной поверхности радиусом  . К колесу в точке В шарнирно присоединен шатун . К колесу в точке В шарнирно присоединен шатун 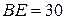 см.
Для заданного положения механизма при см.
Для заданного положения механизма при  с вычислить с вычислить  , ,  . .
| ||||||||||

| 19. Кривошип 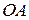 , вращаясь замедленно, приводит в движение ролик 2 радиусом , вращаясь замедленно, приводит в движение ролик 2 радиусом  см, который катится по внутренней поверхности неподвижного колеса 1 радиусом см, который катится по внутренней поверхности неподвижного колеса 1 радиусом 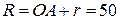 см. К колесу 2 в точке В шарнирно прикреплен шатун см. К колесу 2 в точке В шарнирно прикреплен шатун  см.
Для заданного положения механизма вычислить см.
Для заданного положения механизма вычислить 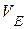 , ,  , если , если  с-1, с-1, 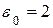 с-2. с-2.
| ||||||||||
20. Кривошип 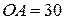 см, вращаясь с см, вращаясь с  (с-1), с помощью шатуна (с-1), с помощью шатуна  м приводит в движение ступенчатый диск с большим и малым радиусами соответственно м приводит в движение ступенчатый диск с большим и малым радиусами соответственно 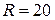 см, см,  см. Диск катится без скольжения по горизонтальной поверхности. Для заданного положения механизма при см. Диск катится без скольжения по горизонтальной поверхности. Для заданного положения механизма при 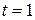 с вычислить с вычислить 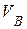 , , 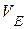 , ,  , , 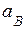 . .
| |||||||||||

| 21. Кривошип 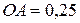 м, вращаясь с угловой скоростью м, вращаясь с угловой скоростью  (с-1), с помощью шатуна (с-1), с помощью шатуна  м приводит в движение ролик 1 радиусом м приводит в движение ролик 1 радиусом 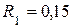 м, который катится без скольжения по неподвижной поверхности 2 радиусом м, который катится без скольжения по неподвижной поверхности 2 радиусом  м равномерно с м равномерно с 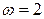 с-1.
Для заданного положения механизма при с-1.
Для заданного положения механизма при  с вычислить с вычислить  , , 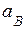 . .
| ||||||||||

| 22. Вычислить скорость точки  четырехзвенного механизма четырехзвенного механизма 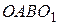 и угловое ускорение шатуна и угловое ускорение шатуна  в положении, указанном на рисунке, если звено в положении, указанном на рисунке, если звено  20 см имеет в данный момент времени угловую скорость 2 рад/с, а точка 20 см имеет в данный момент времени угловую скорость 2 рад/с, а точка  является серединой стержня является серединой стержня  . .
| ||||||||||

| 23. Груз  , связанный посредством нерастяжимой нити с катушкой , связанный посредством нерастяжимой нити с катушкой  , опускается вертикально вниз по закону , опускается вертикально вниз по закону  м. Катушка м. Катушка  катится без скольжения по неподвижному горизонтальному рельсу.
Вычислить скорости точек катится без скольжения по неподвижному горизонтальному рельсу.
Вычислить скорости точек  , , 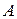 , ,  , ,  и и  катушки в момент катушки в момент 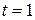 с в положении, указанном на рисунке, и угловую скорость катушки, если с в положении, указанном на рисунке, и угловую скорость катушки, если  , ,  20 см. 20 см.
| ||||||||||
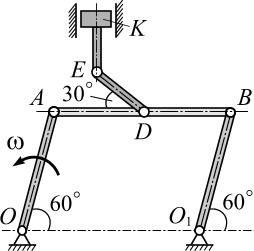
| 24. К середине 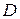 стержня стержня 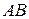 шарнирного параллелограмма шарнирного параллелограмма 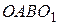 присоединен с помощью шарнира стержень присоединен с помощью шарнира стержень  , приводящий в возвратно-поступательное движение ползун , приводящий в возвратно-поступательное движение ползун  .
Вычислить скорость ползуна .
Вычислить скорость ползуна  и угловую скорость стержня и угловую скорость стержня 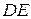 в положении, указанном на рисунке. в положении, указанном на рисунке.  20 см; угловая скорость звена 20 см; угловая скорость звена  равна равна 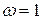 рад/с. рад/с.
| ||||||||||
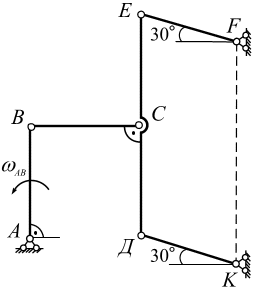
| 25. Рассчитать скорости точек механизма; угловую скорость и угловое усклорение звена 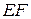 .
Дано: .
Дано:  см, см,  , ,  – шарнирный параллелограмм; – шарнирный параллелограмм;  с-1; в данный момент с-1; в данный момент 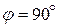 , ,  , , 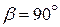 . .
| ||||||||||
Дата добавления: 2015-04-15; просмотров: 696; Мы поможем в написании вашей работы!; Нарушение авторских прав |