
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм решения. Первый тип задач (прямая задача) – заданы уравнения движения точки в плоскости , или , требуется вычислить скорость и ускорен
Первый тип задач (прямая задача) – заданы уравнения движения точки в плоскости  ,
,  или
или 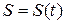 , требуется вычислить скорость и ускорение точки тела; если движение точки задано координатным способом - то вычислить уравнение траектории в явном виде
, требуется вычислить скорость и ускорение точки тела; если движение точки задано координатным способом - то вычислить уравнение траектории в явном виде  .
.
Схема решения:
· выбирают систему координат (  или
или  ) и начало координат (та или иная система выбираются исходя из условий задачи так, чтобы дальнейшее решение было по возможности более простым);
) и начало координат (та или иная система выбираются исходя из условий задачи так, чтобы дальнейшее решение было по возможности более простым);
· на основании условий задачи для избранной системы координат составляют уравнения движения точки (если они явно не заданы), т.е. находят зависимости координат точки от времени –  ,
,  ;
;
· исключая параметр  из уравнений движения, вычисляют траекторию точки как функцию –
из уравнений движения, вычисляют траекторию точки как функцию –  ;
;
· дифференцируя по времени уравнения движения  ,
,  , или
, или 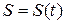 , вычисляют скорость точки;
, вычисляют скорость точки;
· вычисляя вторую производную по времени от  ,
,  , находят ускорение точки;
, находят ускорение точки;
· если движение точки задано естественным способом, т.е. задана траектория движения, радиус кривизны и 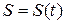 , вычисляют нормальную и касательную составляющие ускорения;
, вычисляют нормальную и касательную составляющие ускорения;
· вычисляют полное ускорение точек по модулю и направлению.
Второй тип задач (обратная задача) - заданы проекции ускорения  ,
,  ; требуется вычислить проекции скорости точки, как функцию времени, т.е.
; требуется вычислить проекции скорости точки, как функцию времени, т.е.  и вычислить уравнения движения точки в декартовой системе координат, т.е.
и вычислить уравнения движения точки в декартовой системе координат, т.е.  ,
,  .
.
Схема решения:
· выбирают систему координат;
· формулируют начальные условия задачи:  ;
;
· разделяют переменные в дифференциальных уравнениях  и
и 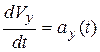 , или
, или  ,
,  и, интегрируя по времени дифференциальные уравнения с разделенными переменными, вычисляют проекции скорости точки
и, интегрируя по времени дифференциальные уравнения с разделенными переменными, вычисляют проекции скорости точки 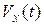 ,
,  , а также уравнения движения точки
, а также уравнения движения точки  ,
,  .
.
J 
| Задачи для самостоятельного решения | |||||

| 1. Положение линейки АВ определяется углом  (рад). Вычислить проекцию скорости точки М на ось Ох в момент времени (рад). Вычислить проекцию скорости точки М на ось Ох в момент времени  с, если расстояние с, если расстояние  м. м.
| |||||

| 2. Положение кривошипа определяется углом 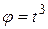 (рад). Вычислить скорость и ускорение ползуна В в момент времени (рад). Вычислить скорость и ускорение ползуна В в момент времени  с, если с, если  м. м.
| |||||
3. Точка движется по прямой с ускорением  (м/с2). Вычислить начальную скорость точки, если через 6 с скорость точки составила 3 м/с. (м/с2). Вычислить начальную скорость точки, если через 6 с скорость точки составила 3 м/с.
| ||||||
4. Проекция скорости точки  . Вычислить координату х точки в момент времени . Вычислить координату х точки в момент времени  с, если в момент времени с, если в момент времени  координата координата  м. м.
| ||||||
5.Точка движется по прямой с ускорением  (м/с2). Вычислить начальную скорость точки, если через 2 с скорость точки составила 6 м/с. (м/с2). Вычислить начальную скорость точки, если через 2 с скорость точки составила 6 м/с.
| ||||||
6. Движение точки задано уравнениями  и и  . Вычислить касательное ускорение в момент времени . Вычислить касательное ускорение в момент времени 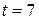 с. с.
| ||||||
7. По заданному уравнению движения точки на произвольно выбранной траектории построить через равные промежутки времени шесть положений точки, определить расстояние  по траектории от начала отсчета до конечного положения точки и пройденный ею путь по траектории от начала отсчета до конечного положения точки и пройденный ею путь  за указанный промежуток времени ( за указанный промежуток времени (  и и  - в сантиметрах, t - в секундах): - в сантиметрах, t - в секундах):
| ||||||
1)  , ,  .
2) .
2)  , ,  .
3) .
3)  , ,  . .
| ||||||
8. По заданным уравнениям движения точки найти уравнения ее траектории в координатной форме и указать на рисунке направление движения:  , , 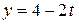 .
1) .
1)  , , 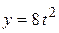 .
2) .
2)  , ,  .
3) .
3)  , , 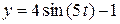 . .
| ||||||
9. Снаряд движется в вертикальной плоскости согласно уравнениям  , , 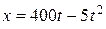 (t – в секундах, х и у – в метрах). Вычислить: скорость и ускорение в начальный момент; высоту и дальность обстрела; радиус кривизны траектории в наивысшей точке. (t – в секундах, х и у – в метрах). Вычислить: скорость и ускорение в начальный момент; высоту и дальность обстрела; радиус кривизны траектории в наивысшей точке.
| ||||||

| 10. Вычислить ускорение точки В в момент времени, когда угол  , если длина , если длина  см, а закон изменения угла см, а закон изменения угла  (рад). (рад).
| |||||

| 11. Положение кривошипа ОА определяется углом  (рад). Вычислить проекции ускорения (рад). Вычислить проекции ускорения  , , 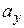 точки А в момент времени точки А в момент времени 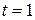 с, если длина кривошипа с, если длина кривошипа  м. м.
| |||||

| 12. Положение линейки АВ определяется углом  (рад). Вычислить проекции ускорения точки М на оси (рад). Вычислить проекции ускорения точки М на оси  и и  в момент времени в момент времени  с, если расстояние с, если расстояние  м. м.
| |||||
13. Точка движется по прямой Ох с ускорением  . Вычислить координату х точки в момент времени . Вычислить координату х точки в момент времени 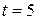 с, если при с, если при  скорость скорость  км/ч, и координата км/ч, и координата  . .
| ||||||
14. Касательное ускорение точки  . Определить момент времени t, когда скорость . Определить момент времени t, когда скорость  точки достигнет 10 м/с, если при точки достигнет 10 м/с, если при  скорость скорость  м/с. м/с.
| ||||||
15. Проекции скорости точки во время движения определяются выражениями  , ,  м/с. Вычислить касательное ускорение в момент времени м/с. Вычислить касательное ускорение в момент времени  с. с.
| ||||||
16. Даны уравнения движения снаряда:
 , ,  ,
где ,
где  - начальная скорость снаряда, - начальная скорость снаряда,  – угол между – угол между  и горизонтальной осью х; g – ускорение силы тяжести. Определить траекторию движения снаряда, высоту Н, дальность L и время Т полета самолета. и горизонтальной осью х; g – ускорение силы тяжести. Определить траекторию движения снаряда, высоту Н, дальность L и время Т полета самолета.
| ||||||

| 17. Из орудия береговой артиллерии с высоты  м над уровнем моря произведен выстрел под углом м над уровнем моря произведен выстрел под углом  к горизонту, начальная скорость снаряда к горизонту, начальная скорость снаряда  м/с. Вычислить, на каком расстоянии от орудия снаряд попадет в цель, находящуюся на уровне моря.
Уравнения движения снаряда в вертикальной плоскости: м/с. Вычислить, на каком расстоянии от орудия снаряд попадет в цель, находящуюся на уровне моря.
Уравнения движения снаряда в вертикальной плоскости:
 , ,
 . .
| |||||
Дата добавления: 2015-04-15; просмотров: 1402; Мы поможем в написании вашей работы!; Нарушение авторских прав |