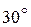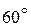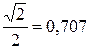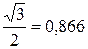КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Координатный способ задания движения точки
| J | Вспомни теорию | G |
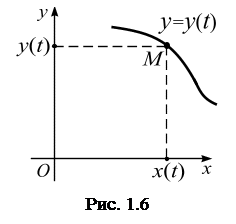 Уравнения движения точки в декартовых прямоугольных координатах имеют вид
Уравнения движения точки в декартовых прямоугольных координатах имеют вид
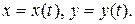 (1)
(1)
Уравнения (1) являются также уравнениями траектории точки, заданными параметрически. Уравнение траектории в системе координат  будет иметь вид функции
будет иметь вид функции  рис. 1.6. Для получения этой зависимости следует из уравнений (1) исключить параметр
рис. 1.6. Для получения этой зависимости следует из уравнений (1) исключить параметр  .
.
Скорость точки. Модуль и направление скорости вычисляются так:
 ,
,  ,
,
здесь 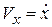 ;
; 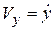 .
.
Ускорение точки. Модуль и направление ускорения вычисляются так:
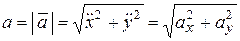 ,
, 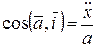 ,
,
здесь 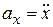 ,
, 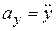 .
.
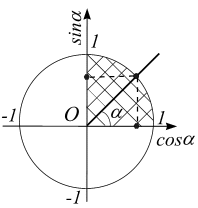
| Справка Значения тригонометрических функций в смысле главного значения | |||||||||||||||||||||||||
| 
|
 Задача 1.2. Движение точки M по плоскости
Задача 1.2. Движение точки M по плоскости  задано уравнениями движения
задано уравнениями движения
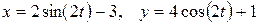 (см). (а)
(см). (а)
Задать движение точки в явном виде 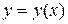 и построить траекторию движущейся точки.
и построить траекторию движущейся точки.
Решение. Дляпостроения траектории движущейся точки в декартовой системе координат определим область, в которой движется точка, т.е. область значений 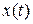 и
и 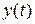 . Функции
. Функции 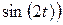 и
и 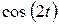 - ограничены, т.е.
- ограничены, т.е.  ,
,  , получаем (см. рис. 1.7):
, получаем (см. рис. 1.7):
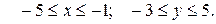
Исключим параметр t из уравнений движения (a). Для этого делим первое уравнение на 2, второе – на 4, возводим их в квадрат и складываем между собой:
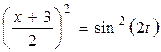
+
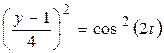
________________________________
 .
.
Учитывая, что 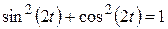 , получим:
, получим:
 . (б)
. (б)
Траекторией движущейся точки является эллипс (рис. 1.7). Подставляя в (а)  , получаем:
, получаем:
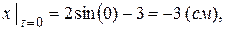
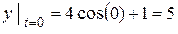 (см).
(см).
Точка в начальный момент времени занимает положение 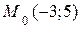 . Определим направление движения точки. Уравнения движения заданы возрастающей функцией
. Определим направление движения точки. Уравнения движения заданы возрастающей функцией  и убывающей функцией
и убывающей функцией  , поэтому при увеличении t координата «х» возрастает, а «у» убывает, следовательно, точка вращается по эллипсу по часовой стрелке (рис. 1.7).
, поэтому при увеличении t координата «х» возрастает, а «у» убывает, следовательно, точка вращается по эллипсу по часовой стрелке (рис. 1.7).
Задача 1.3. Положение кривошипа ОА в кривошипно-ползунном механизме (рис. 1.8) определяется углом  (рад). Вычислить скорость и ускорение точек А и В в моменты
(рад). Вычислить скорость и ускорение точек А и В в моменты  и
и  , если
, если 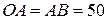 см.
см.
Решение. Декартовую систему координат  совместим с точкой О кривошипа 0А (рис. 1.8).Движение каждой точки данного механизма можно задать координатным способом относительно выбранной системы отсчета, т.е. задать координаты -
совместим с точкой О кривошипа 0А (рис. 1.8).Движение каждой точки данного механизма можно задать координатным способом относительно выбранной системы отсчета, т.е. задать координаты - 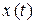 и
и 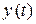 каждой точки.
каждой точки.
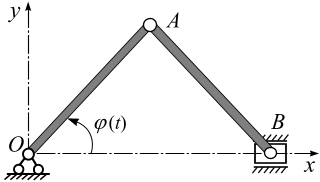
Рис. 1.8
Точка А движется по окружности, радиус которой равен длине кривошипа ОА, точка В – прямолинейно вдоль оси  . Следовательно, в любой момент времени положение точки А определяется координатами
. Следовательно, в любой момент времени положение точки А определяется координатами 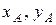 , а движение точки В определяться координатой
, а движение точки В определяться координатой 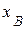 (рис. 1.9).
(рис. 1.9).
Имеем:
 , тогда
, тогда
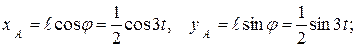
 .
.
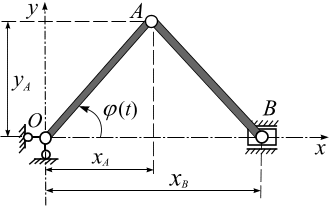
Рис. 1.9
Вычислим скорость и ускорения точек А и В:
Скорость точки А:
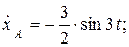
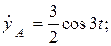
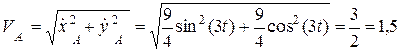 (см/c).
(см/c).
Направление вектора скорости:
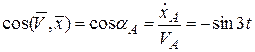 ,
, 
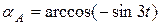 .
.
Модуль скорости точки А в любом положении механизма остается величиной постоянной и равной 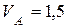 (см/c). Направление вектора скорости (угол
(см/c). Направление вектора скорости (угол 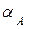 )зависит от положения кривошипа.
)зависит от положения кривошипа.
Скорость точки В:
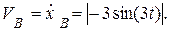
Ускорение точки А:

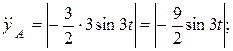
 (см/c).
(см/c).
Знаки  ,
, 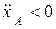 , следовательно, точка А вдоль оси
, следовательно, точка А вдоль оси  движется ускоренно;
движется ускоренно; 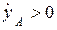 ,
,  – точка А вдоль оси
– точка А вдоль оси  движется замедленно.
движется замедленно.
Направление вектора ускорения:
 ,
, 
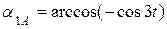 .
.
Ускорение точки В: 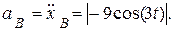
Знаки  ,
, 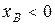 определяют направление движения точки В, т.е. точка В движется против оси
определяют направление движения точки В, т.е. точка В движется против оси  ускоренно.
ускоренно.
1. Вычислим положение механизма и кинематические характеристики точек при  с.Положение механизма определяется углом
с.Положение механизма определяется углом  . Для момента времени
. Для момента времени  с,вычислим значение этого угла (рис. 1.10):
с,вычислим значение этого угла (рис. 1.10):
 .
.
Справка:
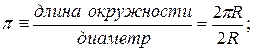 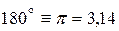 радиан;
1 радиан радиан;
1 радиан  ; ; 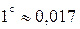 радиан. радиан.
|
Вычислим направление векторов скорости и ускорения точки А:
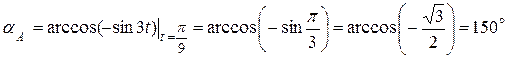 ;
;
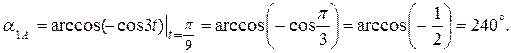
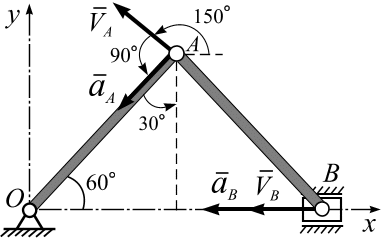
Рис.1.10
Вектор скорости  направлен к оси кривошипа под углом
направлен к оси кривошипа под углом  , вектор ускорения
, вектор ускорения 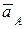 направлен по оси кривошипа, угол между
направлен по оси кривошипа, угол между  и
и 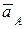 равен
равен  (рис. 1.10).
(рис. 1.10).
Вычислим модули скороси и ускорения точки В:
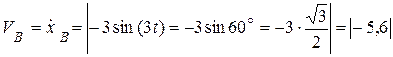 см/c;
см/c;
 см/c2
см/c2
Знаки производных:  ,
,  показывают, что в заданный момент времени точка В движется против оси
показывают, что в заданный момент времени точка В движется против оси  ускоренно (рис. 1.10).
ускоренно (рис. 1.10).
2. Вычислим положение механизма и кинематические характеристики точек при 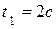 , (рис. 1.11).
, (рис. 1.11).
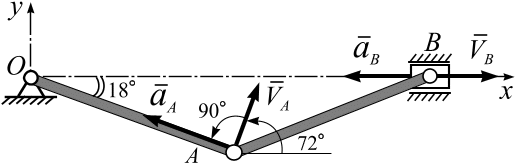
Рис. 1.11
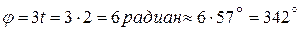 (
(  ).
).
Вычислим направление векторов скорости и ускорения точки А:
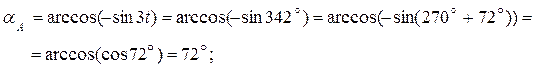
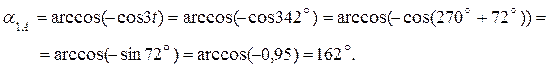
Справка
Формулы приведения:
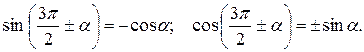
|
Вектор скорости  направлен к оси кривошипа под углом
направлен к оси кривошипа под углом  , вектор ускорения
, вектор ускорения 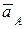 направлен по оси кривошипа, угол между
направлен по оси кривошипа, угол между  и
и 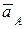 равен
равен  (рис. 1.11).
(рис. 1.11).
Вычислим модули скороси и ускорения точки В:
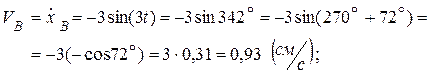
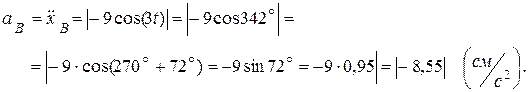
Знаки 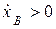 ,
,  показывают, что в заданный момент времени точка В вдоль оси
показывают, что в заданный момент времени точка В вдоль оси  движется замедленно.
движется замедленно.
Ответ: 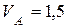 см/c;
см/c;  см/c2;
см/c2;
 :
: 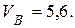 см/c;
см/c; 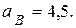 см/c2;
см/c2;
 :
:  см/c;
см/c;  см/c2.
см/c2.
Задача 1.4. Точка движется в плоскости  . Уравнение движения точки задано координатным способом:
. Уравнение движения точки задано координатным способом:
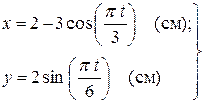 , где
, где  и
и 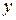 выражены в см,
выражены в см,  - в с. (а)
- в с. (а)
Требуется:
1. Построить траекторию движения точки в декартовой системе координат.
2. Вычислить положение точки в начальный момент времени  , направление движения точки по траектории и положение точки на траектории при
, направление движения точки по траектории и положение точки на траектории при 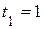 с.
с.
3. Вычислить время цикла движения точки.
4. Вычислить вектор скорости 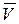 при
при 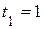 с.
с.
5. Вычислить вектор ускорения  точки при
точки при 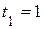 с.
с.
Решение. 1. Построим траекторию движения точки.Дляэтого в декартовой системе координат определим область, в которой движется точка, т.е. область значений 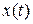 и
и 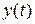 . Функции
. Функции  и
и  - ограничены, т.е.
- ограничены, т.е. 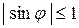 ,
,  , получаем (рис. 1.12):
, получаем (рис. 1.12):
 ;
; 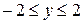 .
.
Получим зависимость  . Для этого из уравнений (а) исключим параметр
. Для этого из уравнений (а) исключим параметр  . Введём обозначение
. Введём обозначение 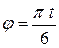 , тогда уравнения (а) перепишутся в виде
, тогда уравнения (а) перепишутся в виде
 (б)
(б)
Распишем первое уравнение системы (б), используя формулу двойного угла (  ), приведем подобные члены и выразим
), приведем подобные члены и выразим  через
через 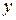 –
–  , получим:
, получим:
 ,
,
или
 . (с)
. (с)
Анализируемтраекторию движения точки. Траекторией точки является парабола с координатой вершины 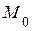 (-1;0); ветви параболы вытянуты вдоль оси
(-1;0); ветви параболы вытянуты вдоль оси  (рис. 1.12).
(рис. 1.12).
Вычислим координаты точки при  :
:
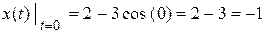 (см);
(см); 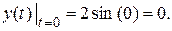
При 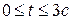 функции
функции 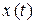 и
и  возрастают (рис. 1.12), точка М из положения
возрастают (рис. 1.12), точка М из положения  начинает движение по верхней ветви параболы до положения
начинает движение по верхней ветви параболы до положения  ; далее при
; далее при  точка движется обратно по верхней ветви траектории до точки
точка движется обратно по верхней ветви траектории до точки  , и при
, и при 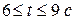 продолжает движение по нижней ветви параболы до положения
продолжает движение по нижней ветви параболы до положения 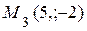 , далее при
, далее при 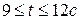 точка возвращается в первоначаьное положение
точка возвращается в первоначаьное положение 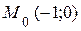 т.е. завершает цикл, далее движение повторяется. Время одного цикла движения
т.е. завершает цикл, далее движение повторяется. Время одного цикла движения  Точка совершает колебательные движения по параболе.
Точка совершает колебательные движения по параболе.
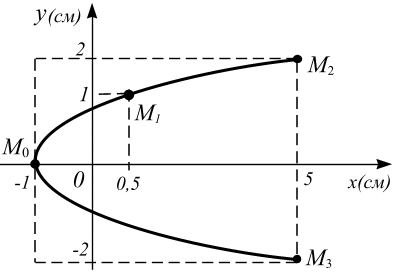
Рис. 1.12
Справка
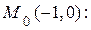 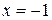 , если , если  , тогда , тогда 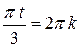 , , 
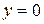 , если , если  , тогда , тогда  , , 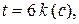
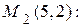 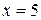 , если , если  , тогда , тогда 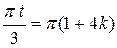 , , 
 , если , , если ,  , тогда , тогда  , , 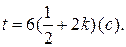
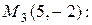 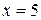 , если , если  , тогда , тогда  , , 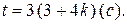
 , если , если 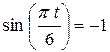 ,тогда ,тогда  , , 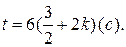 Здесь
Здесь  . .
|
2. Вычислим координаты точки  для фиксированного времени. Для этого подставим значение
для фиксированного времени. Для этого подставим значение  в (а) и вычислим соответствующие координаты:
в (а) и вычислим соответствующие координаты:
при 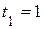 с:
с: 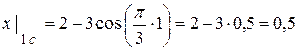 (см);
(см);
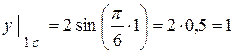 (см).
(см).
3. Вычислим скорость 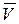 точки
точки 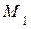 для
для 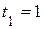 с:
с:
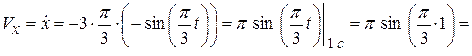
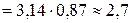 (см/c);
(см/c);
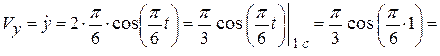
 (см/c);
(см/c);
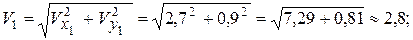 см/с;
см/с;
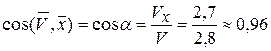 ,
, 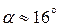 .
.
Откладываем проекции скорости 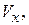
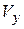 и вектор
и вектор 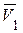 на графике (рис. 1.13).
на графике (рис. 1.13).
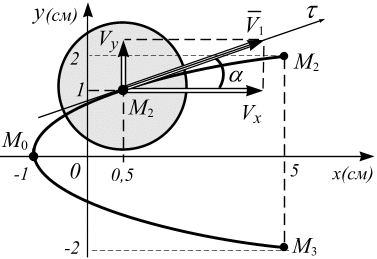
Рис. 1.13
4. Вычислим ускорение  точки
точки  для
для 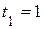 с:
с:

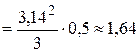 (см/c2);
(см/c2);
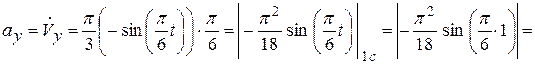
 (см/c2);
(см/c2);
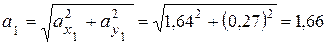 (см/c2);
(см/c2);
 ,
, 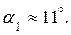
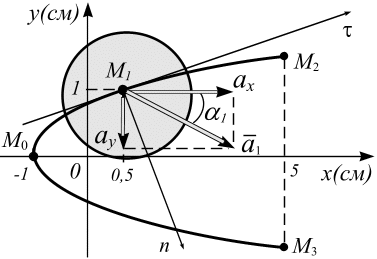
Рис. 1.14
Откладываем проекции ускорения 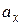 ,
,  и вектор
и вектор  на графике (рис. 1.14).
на графике (рис. 1.14).
Ответ:
1. Точка движется по параболе  в области
в области
 ;
; 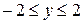 .
.
2. Положение точки на траектории определяется координатами 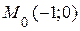 ,
, 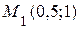 ;
;
3. Скорость точки  см/c; ускорение точки
см/c; ускорение точки 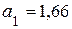 см/c2.
см/c2.
| J | Вспомни теорию | G |
Прямая задача-по заданному уравнению движения 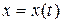 требуется вычислить скорость и ускорение точки:
требуется вычислить скорость и ускорение точки:
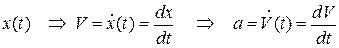 .
.
Если  и
и 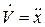 имеют один знак, то вектор скорости и вектор ускорения направлены в одну сторону, тогда движение будет ускоренным; если в противоположные – замедленным.
имеют один знак, то вектор скорости и вектор ускорения направлены в одну сторону, тогда движение будет ускоренным; если в противоположные – замедленным.
Задача 1.5. Прямолинейное движение точки М задано уравнением 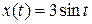 . Вычислить скорость и ускорение точки М в момент времени
. Вычислить скорость и ускорение точки М в момент времени 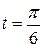 с.
с.
Решение. Траекторией движения точки является отрезок на прямой  (м) (рис. 1.15). Точка начинает движение вправо из координаты
(м) (рис. 1.15). Точка начинает движение вправо из координаты  (
( 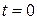 ) до координаты
) до координаты 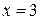
 , далее вектор скорости меняет направление, и точка движется влево до координаты
, далее вектор скорости меняет направление, и точка движется влево до координаты 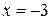
 , и т.д. В момент времени
, и т.д. В момент времени 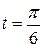 с точка М имеет координату:
с точка М имеет координату:
 м.
м.
Имеем: 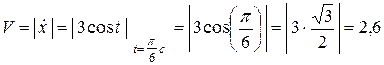 (м/с);
(м/с);
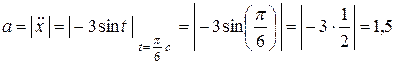 (м/с2).
(м/с2).
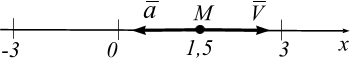
Рис. 1.15
Знаки производных определяют направление векторов 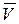 и
и  , поэтому точка в этот момент времени движется замедленно, вектор скорости и вектор ускорения направлены по оси
, поэтому точка в этот момент времени движется замедленно, вектор скорости и вектор ускорения направлены по оси  в противоположные стороны (рис. 1.15).
в противоположные стороны (рис. 1.15).
Ответ:  (м/с);
(м/с);  (м/с2).
(м/с2).
| J | Вспомни теорию | G |
Обратная задача - задано ускорение движущейся точки  и требуется вычислить скорость точки и уравнение движения точки
и требуется вычислить скорость точки и уравнение движения точки  :
:
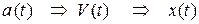 .
.
Ускорение точки связано со скоростью, скорость с координатой дифференциальными уравнениями:
 ,
, 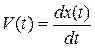 . (2)
. (2)
При решении дифференциальных уравнений (2) разделяют переменные

 , (3)
, (3)
и интегрируют (3) с учетом начальных условий задачи, т.е. значений координаты и скорости в начальный момент времени:
Начальные условия задачи  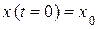 , ,  –
определяют нижние пределы интегрирования –
определяют нижние пределы интегрирования
|

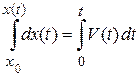 .
.
 При интегрировании уравнений (3) нижние пределы интегрирования соответствуют значениям интегрируемых величин в начальный момент времени, т.е. начальным условиям задачи, верхние пределы интегрирования соответствуютзначению интегрируемых величин при текущем времени t.
При интегрировании уравнений (3) нижние пределы интегрирования соответствуют значениям интегрируемых величин в начальный момент времени, т.е. начальным условиям задачи, верхние пределы интегрирования соответствуютзначению интегрируемых величин при текущем времени t.
Задача 1.6. Точка движется вдоль оси  с ускорением
с ускорением  . В начальный момент времени (
. В начальный момент времени ( 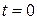 )
)  ,
,  м/c. Вычислить скорость точки через
м/c. Вычислить скорость точки через  с.
с.
Решение. Ускорение и скорость точки связаны между собой дифференциальным уравнением с разделенными переменными:
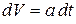 . (а)
. (а)
Начальные условия задачи: 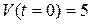 (м/c).
(м/c).
Подставив значение ускорения в (а), получим:

Взяв от обеих частей равенства определенный интеграл с учетом начальных условий задачи, получим величину скорости точки через  с:
с:

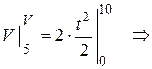


 (м/с).
(м/с).
Ответ:  (м/с).
(м/с).
Дата добавления: 2015-04-15; просмотров: 617; Мы поможем в написании вашей работы!; Нарушение авторских прав |