Мгновенный центр скоростей

В каждый момент времени при плоском движении тела, если , имеется единственная точка в плоскости его движения, скорость которой равна нулю. Эту точку называют мгновенным центром скоростей (МЦС). Обозначают ее обычно точкой Р.

Тогда каждая точка тела будет мгновенно двигаться по окружности, радиус которой определяется расстоянием этой точки до МЦС (рис. 4.4), дуга, по которой пройдет каждая точка тела в единицу времени, будет равна: где - расстояние точки до МЦС, т.е.:

Рис.4.4

Если положение МЦС известно, то, приняв МЦС за полюс ( ), любые точки, например точки А и В (рис. 4.5), будут направлены перпендикулярно радиусу, равному расстоянию от этой точки до точки МЦС:

;

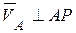Здесь АР и ВР – расстояние от точек А и В до МЦС, т.е. до точки Р.

Следовательно, если положение МЦС известно, то скорости точек тела вычисляют так же, как и в случае вращения тела в плоскости вокруг неподвижного центра:

Частные случаи вычисления точки МЦС.

· Цилиндрическое тело катится по неподвижной поверхности, точка касания Р является МЦС (рис. 4.6, а), т.е. тело мгновенно вращается относительно точки касания Р.

· Скорости точек А и В тела параллельны друг другу, причем линия АВ не перпендикулярна к и (рис. 4.6, б), точка МЦС находится в бесконечности, тогда , т.е. тело движется мгновенно-поступательно.

· Скорости точек А и В тела параллельны друг другу и при этом , положение точки МЦС определяется построениями, показанными на рис. 4.6 в, г; тело совершает мгновенно-вращательное движение вокруг точки Р.

Рис. 4.6

Задача 4.2. Кривошипно-шатунный механизм (рис. 4.7) состоит из кривошипа ОА, шатуна АВ и ползуна В. Кривошип ОА длиной м вращается с угловой скоростью с^-1. Длина шатуна м. При заданном угле вычислить:

1. угловую скорость шатуна АВ – ;

2. скорость ползуна В;

3. рассмотреть положение механизма, когда 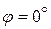и .

а		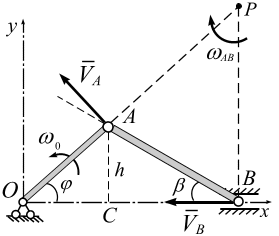б
Рис. 4.7

Решение. Вначале вычислим модуль скорости точки А, принадлежащей кривошипу ОА:

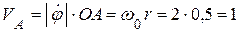(м/с).

Вектор скорости направлен перпендикулярно ОА в сторону вращения кривошипа (рис. 4.7, а).

Вектор скорости ползуна направлен вдоль дорожек. Восстановим перпендикуляры к векторам и . Точка МЦС (точка Р) лежит на их пересечении. Из геометрии задачи вычислим АР и ВР (рис. 4.7, б).

Имеем:

из 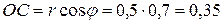м; м;

из

м;

м;

м; м.

Напомним, что угол . Тогда:

; ; .

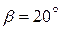Угловая скорость шатуна АВ:

(с^-1).

Если механизм нарисован в масштабе, то АР и ВР измеряются линейкой.

2. Скорость ползуна (скорость в точке В):

(м/с).

Проверим правильность полученных результатов, используя основную теорему кинематики. Имеем (рис. 4.6, б):

угол САВ= ,

тогда, согласно основной теореме кинематики, получаем:

3. Угол (рис. 4.7, а).

Восстановим перпендикуляры к векторам и . Точка МЦС (точка Р) лежит на их пересечении и совпадает с точкой В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей, тогда . В этом положении шатун АВ совершает мгновенное вращение вокруг точки В с угловой скоростью:

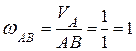(с^-1).

Распределение скоростей шатуна показано на рис. 4.8 а.

Угол (рис. 4.8, б).

а		б
Рис. 4.8

Скорости и направлены параллельно друг другу, и перпендикуляры к ним пересекаются в бесконечности, тогда . Следовательно, в этом положении шатун совершает мгновенно-поступательное движение, и все точки шатуна АВ имеют одинаковую скорость, равную (м/с).

Ответ: (с^-1); (м/с).