
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ускорение при плоском движении твердого тела
Ускорение какой-либо точки тела при его плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении тела вокруг полюса:
 .
.
Здесь:  – ускорение полюса;
– ускорение полюса;
 – ускорение точки В при ее вращении вместе с телом вокруг полюса А:
– ускорение точки В при ее вращении вместе с телом вокруг полюса А:
нормальная составляющая ускорения направлена по нормали, т.е. по АВ к полюсу А, и равна  ;
;
касательная составляющая ускорения направлена ^ АВ в сторону дуговой стрелки  и равна
и равна 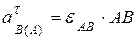
Задача 4.3.Кривошип ОА длиной 60 см вращается ускоренно относительно оси О и приводит в движение ролик 1 радиусом  см, который катится без скольжения по неподвижному колесу 2 (рис. 4.9). Параметры вращения кривошипа в данный момент времени
см, который катится без скольжения по неподвижному колесу 2 (рис. 4.9). Параметры вращения кривошипа в данный момент времени  с-1,
с-1,  с-2. Вычислить угловую скорость
с-2. Вычислить угловую скорость 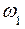 и угловое ускорение
и угловое ускорение  ролика, вычислить скорость и ускорение точки В, находящейся на ролике на расстоянии 10 см от точки А.
ролика, вычислить скорость и ускорение точки В, находящейся на ролике на расстоянии 10 см от точки А.

Рис. 4.9
Решение. Кривошип ОА совершает вращательное движение относительно оси, проходящей через неподвижный центр О. Скорость и ускорение точки А кривошипа вычисляют по формулам
 (см/с);
(см/с);
 .
.
Подвижный ролик движется плоскопараллельно. Вычислим 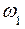 и
и  подвижного ролика. Плоское движение ролика можно привести к мгновенно-вращательному движению относительно мгновенного центра скоростей (МЦС), этим центром является точка касания Р (рис. 4.10).
подвижного ролика. Плоское движение ролика можно привести к мгновенно-вращательному движению относительно мгновенного центра скоростей (МЦС), этим центром является точка касания Р (рис. 4.10).
Запишем уравнение связи между движениями кривошипа и ролика. Точка А одновременно принадлежит кривошипу ОА и ролику 1. Следовательно, перемещение точки А:
 , т.е.
, т.е.  .
.
Угловая скорость и угловое ускорение ролика 1 тогда вычисляются:
 (с-1);
(с-1);
 (с-2).
(с-2).

Рис. 4.10
Угол вращения ролика относительно точки Р (точка МЦС) совпадает с углом вращения кривошипа (рис. 4.9). Направления вращения 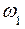 и
и  ролика 1 совпадают, отмечаем их дуговыми стрелками; следовательно, движение ролика 1 является ускоренным, как и кривошипа ОА.
ролика 1 совпадают, отмечаем их дуговыми стрелками; следовательно, движение ролика 1 является ускоренным, как и кривошипа ОА.
Скорость точки В.
Точка В находится на ролике 1, следовательно, её скорость определяется как скорость точки, вращающейся вокруг МЦС, т.е. точки Р:
 .
.
Из геометрии задачи определим по теореме косинусов расстояние ВР:

 (см).
(см).
Тогда скорость точки В:
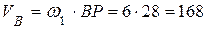 (см/с).
(см/с).
Вектор  перпендикулярен отрезку ВР и направлен в сторону вращения
перпендикулярен отрезку ВР и направлен в сторону вращения 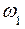 ролика (рис. 4.10).
ролика (рис. 4.10).
Ускорение точки В.
Ускорение точки В складывается из ускорения полюса и ускорения точки В при её вращении вместе с роликом вокруг этого полюса. За полюс примем точку А, т.к. её ускорение известно.
Тогда ускорение точки В запишется (рис. 4.11):
 .
.
| а | 
| б | 
|
| Рис. 4.11 |
Здесь:
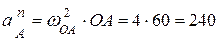 (см/с2) - нормальная составляющая ускорения полюса, направлена от точки А к центру О;
(см/с2) - нормальная составляющая ускорения полюса, направлена от точки А к центру О;
 (см/с2) - касательная составляющая ускорения полюса, направлена перпендикулярно
(см/с2) - касательная составляющая ускорения полюса, направлена перпендикулярно  в сторону углового ускорения кривошипа ОА -
в сторону углового ускорения кривошипа ОА -  ;
;
 (см/с2) - ускорения точки В при её вращении относительно полюса А; вектор
(см/с2) - ускорения точки В при её вращении относительно полюса А; вектор  перпендикулярен АВ и направлен по направлению дуговой стрелки
перпендикулярен АВ и направлен по направлению дуговой стрелки  ;
;
 (см/с2), вектор
(см/с2), вектор  направлен по отрезку АВ от точки В к точке А.
направлен по отрезку АВ от точки В к точке А.
Выражение для расчета ускорения точки В записано в векторной форме. Для аналитических вычислений необходимо спроецировать это векторное равенство на две оси координат, тогда теорема примет вид
 , где
, где

 (см/с2);
(см/с2);

 (см/с2).
(см/с2).
Модуль ускорения точки В вычислим по формуле
 (см/с2).
(см/с2).
Для определения направления вектора полного ускорения точки В строится параллелограмм на его проекциях  и
и  , диагональ этого параллелограмма и будет вектором ускорения точки В (рис. 4.11).
, диагональ этого параллелограмма и будет вектором ускорения точки В (рис. 4.11).
Ответ: 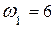 (с-1),
(с-1),  (с-2);
(с-2);  (см/с);
(см/с);  (см/с2).
(см/с2).
Задача 4.4. В кривошипно-шатунном механизме кривошип ОА длиной 40 см вращается замедленно относительно центра О, с угловой скоростью  с-1 и угловым ускорением
с-1 и угловым ускорением  с-2 (рис. 4.12), и приводит в движение шатун АВ длиной 80 см.
с-2 (рис. 4.12), и приводит в движение шатун АВ длиной 80 см.

Рис. 4.12
Вычислить:
1. скорость и ускорение точки В ползуна;
2. скорость и ускорение точки С, расположенной на шатуне АВ на расстоянии  см.
см.
Решение. В кривошипно-шатунном механизмекривошип ОА вращается относительно центра О, шатун АВ движется плоскопараллельно, ползун В движется поступательно.
Точка А одновременно принадлежит и кривошипу ОА, и шатуну АВ. Рассматривая вращение кривошипа, скорость точки А рассчитываем по формуле:
 (см/с).
(см/с).
Вектор скорости  перпендикулярен кривошипу ОА и направлен в сторону угловой скорости кривошипа. Вектор скорости точки В шатуна направлен вдоль направляющих ползуна, в данном случае - по горизонтали (рис. 4.12).
перпендикулярен кривошипу ОА и направлен в сторону угловой скорости кривошипа. Вектор скорости точки В шатуна направлен вдоль направляющих ползуна, в данном случае - по горизонтали (рис. 4.12).
Заменим плоское движение шатуна АВ мгновенно-вращательным относительно мгновенного центра скоростей (МЦС). Для нахождения МЦС восстановим перпендикуляры к построенным векторам скоростей  и
и  , на их пересечении будет находиться МЦС шатуна - точка Р (рис. 4.13, а).
, на их пересечении будет находиться МЦС шатуна - точка Р (рис. 4.13, а).
| а | 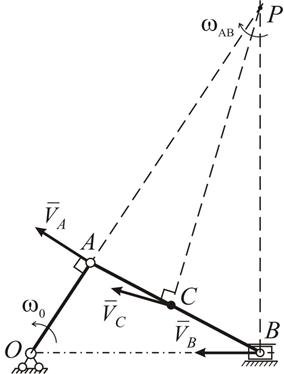
| б | 
|
| Рис. 4.13 |
Направление мгновенного вращения шатуна АВ вокруг МЦС -  - определяем по направлению вектора
- определяем по направлению вектора  .
.
Величина угловой скорости шатуна рассчитывается:
 , откуда:
, откуда:
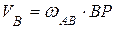 ,
,  .
.
Если положение кривошипно-шатунного механизма фиксировано и начерчено в масштабе, то расстояния ВР и СР измеряются с чертежа линейкой. В общем случае рассматривают геометрию задачи (рис. 4.13, б).
Для вычисления расстояний АР, ВР, СР рассмотрим треугольники ОАВ и ОРВ:
из 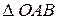 по теореме синусов:
по теореме синусов:


 ;
;
 ;
; 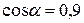 ,
,  ;
;
из 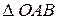 по теореме синусов:
по теореме синусов:
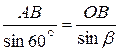 ;
;  ;
;
 см.
см.
В прямоугольном треугольнике  угол ОРВ равен
угол ОРВ равен  , поэтому гипотенуза ОР равна удвоенному произведению катета ОВ, лежащего против угла
, поэтому гипотенуза ОР равна удвоенному произведению катета ОВ, лежащего против угла  :
:
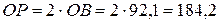 см, тогда
см, тогда  см.
см.
По теореме Пифагора расстояние ВР:
 см.
см.
Расстояние СР определяется из  по теореме косинусов, с учетом угла
по теореме косинусов, с учетом угла  :
:

 см.
см.
Угловая скорость шатуна АВ, скорости точек В и С вычисляют следующим образом:
 ,
,
откуда 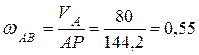 с-1;
с-1;
 (см/с),
(см/с),
 (см/с).
(см/с).
Вектор скорости 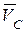 перпендикулярен отрезку РС и направлен в сторону мгновенного вращения шатуна
перпендикулярен отрезку РС и направлен в сторону мгновенного вращения шатуна  (рис. 4.13, а).
(рис. 4.13, а).
Рассчитываем ускорение точки В ползуна. Принимаем точку А шатуна за полюс, тогда
 . (а)
. (а)
Здесь (рис. 4.14, а):
 - ускорение полюса А:
- ускорение полюса А:

 (см/с2) ;
(см/с2) ;
 (см/с2);
(см/с2);
 - ускорение точки В при ее вращении вокруг полюса А:
- ускорение точки В при ее вращении вокруг полюса А:

 (см/с2),
(см/с2),
 .
.
Вектор  направлен по шатуну АВ от точки В к точке А; вектор
направлен по шатуну АВ от точки В к точке А; вектор  располагаем перпендикулярно шатуну АВ.
располагаем перпендикулярно шатуну АВ.
Сводим вектора  ,
,  ,
,  ,
,  в точку В (рис. 4.14, б).
в точку В (рис. 4.14, б).
| а | б |

| 
|
Рис. 4.14
Ускорение точки В определяется векторным уравнением:
 . (б)
. (б)
Таким образом, получили векторное равенство с двумя неизвестными:  и
и 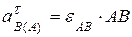 .
.
Вычислить  и
и  можно двумя способами - аналитическим и геометрическим. Рассмотрим каждый из указанных способов.
можно двумя способами - аналитическим и геометрическим. Рассмотрим каждый из указанных способов.
Аналитический способ. Начало декартовой системы координат совместим с точкой В, ось  с осью ползуна, ось
с осью ползуна, ось  перпендикулярна оси ползуна (рис. 4.14, б). Вектор ускорения ползуна
перпендикулярна оси ползуна (рис. 4.14, б). Вектор ускорения ползуна  направлен вдоль оси
направлен вдоль оси  , поэтому проекция вектора
, поэтому проекция вектора  на ось
на ось  равна нулю:
равна нулю:
– из (б) получаем:
 ,
,  ;
;
 ;
;



 с-2;
с-2;

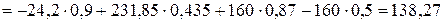 (см/с2);
(см/с2);
 (см/с2).
(см/с2).
Здесь  ,
,  .
.
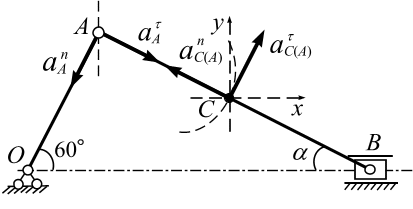
Вычислим ускорение точки С. Положительный знак  означает, что выбранное на схеме направление этого вектора совпадает с истинным. Следовательно, угловое ускорение шатуна
означает, что выбранное на схеме направление этого вектора совпадает с истинным. Следовательно, угловое ускорение шатуна  направлено против часовой стрелки (рис. 4.15, а).
направлено против часовой стрелки (рис. 4.15, а).
| а | б |
| 
|
Рис. 4.15
Ускорение точки С:
 ,
,
где 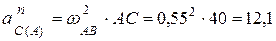 (см/с2),
(см/с2),
 (см/с2).
(см/с2).
Спроецируем записанное векторное равенство на оси  и Сy (рис. 4.14, б):
и Сy (рис. 4.14, б):

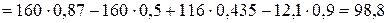 (см/с2);
(см/с2);

 (см/с2).
(см/с2).
Модуль ускорения точки С:
 (см/с2).
(см/с2).
Геометрический (графический) способ

Рис. 4.16
Ускорение ползуна В можно получить построением многоугольника ускорений (рис. 4.16). Для этого в принятом масштабе откладываем из точки В ускорение  , далее, перпендикулярно ему, откладываем касательную составляющую ускорения полюса
, далее, перпендикулярно ему, откладываем касательную составляющую ускорения полюса  , под углом
, под углом  к горизонту откладываем ускорение
к горизонту откладываем ускорение  , из его конца проводим пунктирную прямую, перпендикулярную
, из его конца проводим пунктирную прямую, перпендикулярную  (параллельную неизвестному ускорению
(параллельную неизвестному ускорению  ) до пересечения с осью
) до пересечения с осью  , по которой направлен вектор ускорения ползуна В. Точка пересечения пунктирной прямой и осью
, по которой направлен вектор ускорения ползуна В. Точка пересечения пунктирной прямой и осью  определяет вектора
определяет вектора  и
и  . Вектор
. Вектор  замыкает многоугольник (рис. 4.16).
замыкает многоугольник (рис. 4.16).
Измеряем длины этих векторов и с учетом масштаба получаем соответственно:
 (см/с2),
(см/с2),  (см/с2).
(см/с2).
Для вычисления ускорения точки С – середины шатуна АВ – соединим концы ускорений точек А и В (рис. 4.16) отрезком  , разделим его пополам точкой
, разделим его пополам точкой  и, соединив точки С и
и, соединив точки С и  , получим вектор ускорения середины шатуна
, получим вектор ускорения середины шатуна  . Замерив его с учетом масштаба, получим
. Замерив его с учетом масштаба, получим 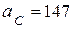 (см/с2).
(см/с2).
Ответ:  с-1,
с-1, 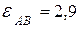 с-2;
с-2; 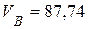 (см/с),
(см/с), 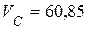 (см/с);
(см/с);
 (см/с2),
(см/с2),  (см/с2).
(см/с2).
Задача 4.5. Вычислить аналитически и графически ускорение шарнира В шарнирного параллелограмма в его данном положении (рис. 4.17 а), если кривошип  см вращается равномерно относительно центра О с угловой скоростью
см вращается равномерно относительно центра О с угловой скоростью  с-1; длины звеньев
с-1; длины звеньев  см,
см,  см.
см.
| а |

| б | 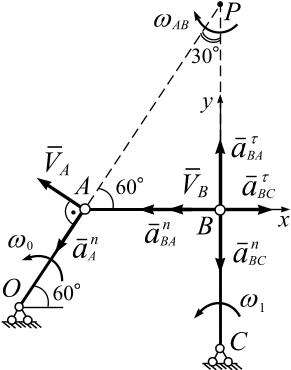
|
| Рис. 4.17 |
Решение. Вычислим угловые скорости звеньев 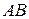 -
-  – и
– и  -
-  :
:
 ,
,  ;
;
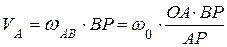 ,
, 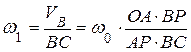 ,
,
Здесь точка Р - точка мгновенного центра скоростей шатуна АВ. Его положение определяется точкой пересечения перпендикуляром к векторам скоростей точек А и В (рис. 4.17, б).
Из  определяем расстояния составляют:
определяем расстояния составляют: 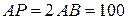 см;
см;  см; тогда:
см; тогда:
 (с-1);
(с-1);
 (с-1).
(с-1).
Аналитический способ
Применим теорему об ускорениях при плоском движении тела к точке В. За полюс выбираем точку А, ускорение в этой точке известно:
 (см/с2);
(см/с2);
тогда:  , (а)
, (а)
здесь  (см/с2);
(см/с2); 
В полученном векторном уравнении (а) три неизвестных: модуль и направление ускорения в точке В -  и угловое ускорение шатуна АВ -
и угловое ускорение шатуна АВ -  (
(  ).
).
Для решения задачи необходимо записать еще одно уравнение. За второй полюс выберем точку  ,
,  , тогда (рис. 4.17 б):
, тогда (рис. 4.17 б):
 , (б)
, (б)
здесь  (см/с2);
(см/с2); 
В полученном векторном равенстве (б) тоже три неизвестных: модуль и направление ускорения в точке В -  и угловое ускорение кривошипа
и угловое ускорение кривошипа  -
-  (
(  ).
).
Получили систему уравнений:
 (в)
(в)
Исключим вектор  из (в). Для этого приравняем правые части уравнений (в) между собой, получим следующее векторное уравнение, которое будет содержать только две неизвестные величины –
из (в). Для этого приравняем правые части уравнений (в) между собой, получим следующее векторное уравнение, которое будет содержать только две неизвестные величины –  и
и  :
:
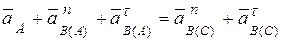 . (г)
. (г)
Совместим с точкой В начало декартовой системы координат (рис. 4.18, а), и спроецируем равенство (г) на эти оси:
 ; (1)
; (1)
 . (2)
. (2)
Получили систему двух скалярных уравнений с двумя неизвестными:  и
и  . Решая последовательно уравнения (1-2), получаем:
. Решая последовательно уравнения (1-2), получаем:
 (см/с2);
(см/с2);
 (см/с2).
(см/с2).
| а | 
| б | 
|
| Рис. 4.18 |
Знак (-) модуля  показывает, что истинное направление этого вектора противоположно выбранному на схеме (рис. 4.18, б).
показывает, что истинное направление этого вектора противоположно выбранному на схеме (рис. 4.18, б).
Вычислим ускорение точки В:
 (см/с2).
(см/с2).
Направление вектора  получаем построением параллелограмма на векторах
получаем построением параллелограмма на векторах  и
и  (рис. 4.18, б).
(рис. 4.18, б).
Графический (геометрический) способ
Ускорение шарнира В получим построением многоугольника ускорений (рис. 4.19). Рассмотрим векторное равенство (г):
 ,
,
здесь:
 (см/с2),
(см/с2),  (см/с2),
(см/с2),  (см/с2).
(см/с2).
В выбранном масштабе откладываем из точки В, параллельно ОА, ускорение  . Из конца этого вектора в том же масштабе, параллельно оси звена АВ, откладываем нормальную составляющую ускорения
. Из конца этого вектора в том же масштабе, параллельно оси звена АВ, откладываем нормальную составляющую ускорения  , и из его конца проводим пунктирную прямую I-I, перпендикулярную
, и из его конца проводим пунктирную прямую I-I, перпендикулярную  (параллельную неизвестному ускорению
(параллельную неизвестному ускорению  ). Затем из точки В, в том же масштабе, откладываем нормальную составляющую ускорения
). Затем из точки В, в том же масштабе, откладываем нормальную составляющую ускорения 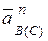 - вдоль звена ВС, из конца этого вектора проводим перпендикулярную ему пунктирную прямую II-II, параллельную неизвестному ускорению
- вдоль звена ВС, из конца этого вектора проводим перпендикулярную ему пунктирную прямую II-II, параллельную неизвестному ускорению  (рис. 4.19).
(рис. 4.19).
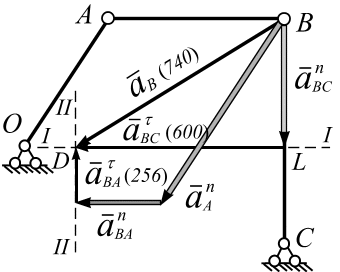
Рис. 4.19
Обозначим точку пересечения прямых I-I и II-II буквой D. Соединим точку В и точку D, полученная прямая  соответствует ускорению точки В -
соответствует ускорению точки В -  ; прямая
; прямая  соответствует ускорению
соответствует ускорению  ; прямая
; прямая  соответствует ускорению
соответствует ускорению  . Замеряем длину отрезков, с учетом принятого масштаба, получаем:
. Замеряем длину отрезков, с учетом принятого масштаба, получаем:
 (см/с2);
(см/с2);  (см/с2);
(см/с2);  см/с2).
см/с2).
Результаты получены двумя разными способами, хорошо согласуются друг с другом.
Ответ: 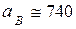 (см/с2).
(см/с2).
Дата добавления: 2015-04-15; просмотров: 684; Мы поможем в написании вашей работы!; Нарушение авторских прав |