Решение. Обозначим через х долю дорогостоящих ЛКС в выручке фармацевтической фирмы, через у — прибыль этой фирмы

Обозначим через х долю дорогостоящих ЛКС в выручке фармацевтической фирмы, через у — прибыль этой фирмы. Кор­реляционная зависимость между у и х прямолинейна, уравнение perрессии имеет вид Для нахождения параметров этого уравнения а₀ и a_t решаем систему нормальных урав­нений:

Значения и приведены в таблице:

х	у	х2	ху		у2
34,00	1200,00	1156,00	40 800,00	1468,97	1 440 000,00
38,00	1820,00	1444,00	69 160,00	1847,65	3 312 400,00
30,50	950,00	930,00	28 975,00	1137,63	902 500,00
28,60	760,00	817,96	21 736,00	957,75	577 600,00
20,70	129,00	428,49	2 670,30	209,86	16 641,00
22,30	650,00	497,29	14 495,00	361,33	422 500,00
35,60	1450,00	1267,36	51620,00	1620,44	2102 500,00
40,50	2100,00	1640,25	85 050,00	2084,33	4410 000,00
45,70	2670,00	2088,49	122 019,00	2576,61	7128 900,00
38,80	1950,00	1505,44	75 660,00	1923,39	3802 500,00
36,70	1810,00	1346,89	66 427,00	1724,58	3276 100,00
32,60	1760,00	1062,76	57 376,00	1336,43	3097 600,00
ИТОГО:
404,00	17 249,00	14 185,18	635 988,30	17 248,96	30 489 241,00

Система нормальных уравнений имеет вид:

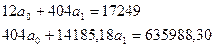
Найдем параметры а₀ и а₁ одним из известных способов:

а₀ = -1749,81, а₁= 94,67.

Следовательно, -1749,81 + 94,67х.

Подставляя в это уравнение соответствующие значения х, полу­чим у _х.

Для измерения тесноты связи между х и у рассчитаем линей­ный коэффициент корреляции:

из таблицы видно, что = 404/12 = 33,67; = 17249/12 = 1437,42; =

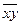635988,30/12 = 52999,03; = 14185,18/12 = 1182,1; = 30489241/12 = 2540770,08.

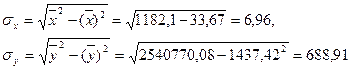
Подставляя эти значения в формулу для линейного коэффициен­та корреляции, получим:

Если коэффициент корреляции исчислен для сравнительно не­большого числа наблюдений (и), следует оценить его надежность (зна­чимость). Для этого рассчитаем среднюю ошибку коэффициента кор­реляции:

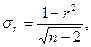
В этой формуле — 2 = 12 — 2 = 10 - число степеней свободы (k).
Итак,

Находим отношение коэффициента корреляции к его средней ошибке:

По таблице в приложении 1 определяем критическое значение t-критерия Стьюдента при числе степеней свободы k =10 и уровне значимости а = 0,05. Оно равно 2,2281. Поскольку, фактическое t больше критического (48 > 2,2281), линейный коэффициент корре­ляции является значимым, а связь между х и у реальной.

Рассчитаем коэф­фициент детерминации d = r² = 0,96² = 0,92.

Таким образом, в результате анализа установлено:

1) существует довольно тесная связь между прибылью фармацевтической фирмы и долей дорогостоящих ЛКС в ее товарообороте (посколь­ку линейный коэффициент корреляции близок к 1);

2) эта связь прямая (поскольку линейный коэффициент корреляции положителен);

3) величина прибыли на 92% зависит от доли дорогостоящих ЛКС в ее товарообороте и на 8% от других факторов.