Определение скорости точек с помощью МЦС

При решении задач пользоваться теоремой о сложении скоростей неудобно, поэтому используют понятие мгновенного центра скоростей (МЦС).

МЦС − это точка, скорость которой в данный момент времени равна 0.

Если в качестве полюса взять МЦС (т. Р), то теорема о сложении скоростей примет вид 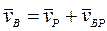, или ; но = 0, тогда , . Таким образом, скорость любой точки плоской фигуры может быть определена как скорость вращения этой точки вокруг МЦС, тогда v_C = ω·АР, v_B= ω ·BР, ... , v_C = ω ·СР ; то есть при определении скоростей можно считать, что тело вращается вокруг МЦС.

МЦС находится на пересечении перпендикуляров к скоростям двух точек тела (рис. 16). Если известна величина одной из скоростей, то можно найти угловую скорость и скорость любой точки сечения по формулам, ω = v_A /АР, v_B= ω ∙ ВР, v_C=ω ∙ СР, ... . Очевидно, что чем ближе точка расположена к мцс, тем меньше ее скорость. Кроме того, v_B / ВР = v_C / СР = … = v_A / АР = ω.

Если скорости двух точек тела параллельны, а перпендикуляры к скоростям не совпадают, то они пересекутся в бесконечности ( рис. 17), в этом случае

ω = v /АР= v /∞ = 0. Говорят, что тело совершает мгновенное поступательное движение. В этом случае скорости всех точек тела равны и параллельны.

Если скорости двух точек тела параллельны, а перпендикуляры к скоростям совпадают, то для определения положения МЦС надо знать величины скоростей двух точек тела. В этом случае МЦС находится на пересечении перпендикуляра к скоростям и линии, проходящей через концы векторов скоростей (рис.18). Расстояние от т. В до МЦС можно определить из подобия треугольников АаР и ВbР: v_A/v_B = (АВ+ВР)/ВР. Отсюда ВР = v_B ∙АВ / ( v_A - v_B). Зная ВР, можно найти ω = v_B / ВР, а затем скорость любой точки. например: v_C = ω · СР. Аналогично решается задача в случае, когда скорости двух точек параллельны и направлены в противоположные стороны.

МЦС тела, катящегося без скольжения по неподвижной поверхности, находится в точке соприкосновения тела и поверхности (рис.19). В этом случае надо знать скорость хотя бы одной точки, тогда ω = v_A/АР; v_B= ω ∙ ВР и т.д.