Задача К1

По заданным уравнениям движения точки в плоскости xy: 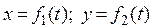(табл. К1) требуется найти уравнение траектории и для момента времени t₁ = π/6 c определить скорость и ускорение точки, а также ее касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории. Построить на рисунке все найденные скорости и ускорения в соответствующих масштабах.

Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются: скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорения точки. В данной задаче все искомые величины нужно определить только для момента времени t₁ = π/6 c. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует применить известные из тригонометрии формулы:

При выборе масштабов построения траектории, скоростей и ускорений следует учитывать, что масштабы должны быть стандартными, то есть из ряда: 1, 2 , 25 , 4 , 5. При этом изображаемые векторы должны быть достаточно крупными (50 - 100 мм).

Таблица К1

Последняя цифра шифра	Предпоследняя цифра шифра
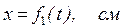
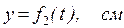
	3sin(2t) + 1		2 - 2cos(2t)
	2sin2(2t) -2		3cos2(2t)-1
	4sin(2t) - 1		2cos(4t) +2
	3 -4 cos(2t)		3sin(2t) - 1
	4cos2(2t)-2		2sin2(2t) + 1
	cos(4t) +1		2sin(2t) - 3
	2sin2(2t) -1		3 - 2cos(2t)
	2cos(4t) + 1		2cos(4t) +1
	3cos2(2t)-2		2sin2(2t)+1
	2+3cos(4t)		2 – 2cos(4t)

Пример К1. Даны уравнения движения точки в плоскости xy:

(x, y – в сантиметрах, t - в секундах).

Определить уравнение траектории точки; для момента времени t₁ = 1c найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Решение. 1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу

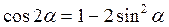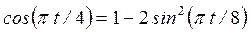или (1)

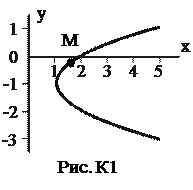Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим:

следовательно,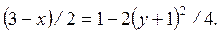

Отсюда окончательно находим следующее уравнение траектории точки (рис. К1):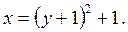

2. Определяем положение точки в заданный момент времени.

при t = 1c: 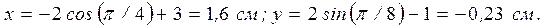Изображаем эту точку на рисунке (т.М).

3. Скорость точки найдем по ее проекциям на координатные оси.

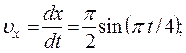
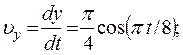
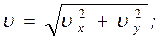
при t = 1c:

4. Аналогично найдем ускорение точки:

.

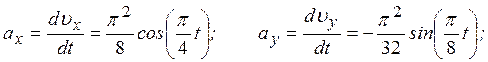
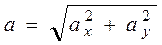при t = 1c: a_x = 0,87 см/с², a_y = - 0,12 см/с², a = 0,88 см/с².

5. Касательное ускорение найдем, дифференцируя по времени равенство . Получим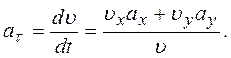

Подставив полученные ранее значения, найдем, что при t = 1c a_τ = 0,66 см/с².

5. Нормальное ускорение точки 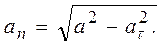Подставляя сюда найденные числовые значения a и a_τ, получим, что при t = 1 c: a_n = 0,58 см/с².

6. Радиус кривизны траектории 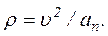Подставляя сюда числовые значения v и a_n , найдем, что при t = 1 c ρ = 3,05 см.

При построении скоростей следует в данном случае выбрать масштаб:

μ_v = 0,02 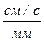, тогда l _vx = │v_x │ / μ_v ≈ 56 мм; l _vy = │v_y │ / μ_v ≈ 37 мм;

или μ_v = 0,01 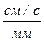, тогда l _vx = │v_x │ / μ_v = 111 мм, l _vy = │v_y │ / μ_v = 73 мм.

При построении ускорений следует выбрать масштаб:

μ_a = 0,01 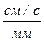, тогда:

l _ax = │a_x │ / μ_a = 0,87/0,01 = 87 мм, l _ay = │a_y │ / μ_a = 0,12/0,01 = 12 мм;

l _aτ = │a_τ │ / μ_a = 0,66/0,01 = 66 мм, l _an = │a_n │ / μ_a = 0,58/0,01 = 58 мм.

Найденные длины отрезков откладываем из точки М.

Примечание.при построении следует учесть, что l _ay необходимо отложить вниз, так как: a_y < 0, а a_τ – по направлению скорости, т. к. a_τ > 0.